In this lesson, we will prove that in a parallelogram, each diagonal bisects the other diagonal.
A line that intersects another line segment and separates it into two equal parts is called a bisector.
In a quadrangle, the line connecting two opposite corners is called a diagonal. We will show that in a parallelogram, each diagonal bisects the other diagonal.
Problem
ABCD is a parallelogram, and AC and BD are its two diagonals. Show that AO = OC and that BO = OD
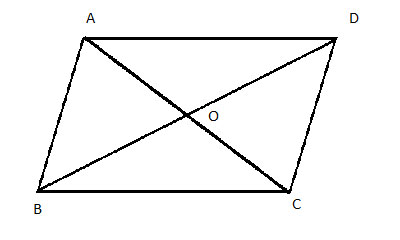
Strategy
Once again, since we are trying to show line segments are equal, we will use congruent triangles. And here, the triangles practically present themselves. Let's start with showing that AO is equal in length to OC, by using the two triangles in which AO and OC are sides: ΔAOD and ΔCOB.
There are all sorts of equal angles here that we can use. Several pairs of (equal) vertical angles, and several pairs of alternating angles created by a transversal line intersecting two parallel lines. So finding equal angles is not a problem. But we need at least one side, in addition to the angles, to show congruency.
As we have already proven, the opposite sides of a parallelogram are equal in size, giving us our needed side.
Once we show that ΔAOD and ΔCOB are congruent, we will have the proof needed, not just for AO=OC, but for both diagonals, since BO and OD are also corresponding sides of these same congruent triangles.
Proof
(1) ABCD is a parallelogram //Given
(2) AD || BC //From the definition of a parallelogram
(3) AD = BC //Opposite sides of a parallelogram are equal in size
(4) ∠OBC ≅ ∠ODA //Alternate Interior Angles Theorem
(5) ∠OCB ≅ ∠OAD //Alternate Interior Angles Theorem
(6) ΔOBC ≅ ΔODA // Angle-Side-Angle
(7) BO=OD // Corresponding sides in congruent triangles (CPCTC)
(8) AO=OC // Corresponding sides in congruent triangles (CPCTC)
The converse of this theorem is also true - if the diagonals of a quadrilateral bisect each other, then that quadrilateral is a parallelogram.