A quadrilateral whose diagonals bisect each other is a parallelogram, as we will show in this exercise. One of the properties of a parallelogram is that its diagonals bisect each other. This is a converse theorem - that shows that if the diagonals bisect each other, the quadrilateral must be a parallelogram.
Problem
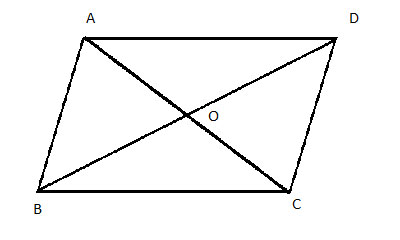
ABCD is a quadrilateral with diagonals AC and BD. The diagonals bisect each other: AO = OC and BO = OD. Show that ABCD is a parallelogram.
Strategy
To prove that ABCD is a parallelogram we need to show that both pairs of the opposite sides are parallel to each other. That is the definition of a parallelogram.
To show that lines are parallel, we can use the Converse Alternate Interior Angles Theorem. This converse theorem states that if the interior alternating angles created by the transversal line are congruent, then the two lines intersected by the transversal line are parallel. And to show that angles are congruent, we'll use congruent triangles.
Step 1
The triangles practically present themselves in the above drawing. Let's look at triangles ΔAOD and ΔCOB. We have two pairs of equal sides: AO = OC and BO = OD. And conveniently, the angles between those two sides (∠AOD , ∠COB) are opposite (vertical) angles, so they are also congruent.
Triangles ΔAOD and ΔCOB are thus congruent using the Side-Angle-Side postulate. From this, we have ∠OBC≅ ∠ODA as corresponding angles in congruent triangles. ∠OBC and ∠ODA are also alternating interior angles formed by the transversal line segment BD which intersects lines AD and BC. So AD||BC using the Converse Alternate Interior Angles Theorem.
Step 2
Now let's look at another pair of triangles, ΔAOB and ΔCOD. Again, we know AO = OC and BO = OD. The angles between those two sides (∠AOB, ∠COD) are opposite (vertical) angles, so they are also congruent. Triangles ΔAOB and ΔCOD are thus congruent using the Side-Angle-Side postulate.
And so, we now have a quadrilateral with two pairs of opposite sides which are parallel. By definition, that is a parallelogram. This proves that the quadrilateral whose diagonals bisect each other is a parallelogram.
From this, we have ∠BAO≅ ∠DCO as corresponding angles in congruent triangles. ∠OBC and ∠ODA are also alternating interior angles, formed by the transversal line segment AC, which intersects lines AB and DC. So AB||DC using the Converse Alternate Interior Angles Theorem.
Proof
(1) AO = OC //Given, ABCD is a quadrilateral whose diagonals bisect each other
(2) BO = OD //Given, ABCD is a quadrilateral whose diagonals bisect each other
(3) ∠AOD≅∠COB // Vertical angles are congruent
(4) ΔAOD ≅ ΔCOB //(1),(2),(3), Side-Angle-Side postulate
(5) ∠OBC≅ ∠ODA //(4) , Corresponding angles in congruent triangles (CPCTC)
(6) AD||BC //(5), Converse Alternate Interior Angles Theorem.
(7) ∠AOB≅∠COD // Vertical angles are congruent
(8) ΔAOB ≅ ΔCOD //(1),(2),(7), Side-Angle-Side postulate
(9) ∠BAO≅ ∠DCO //(8) , Corresponding angles in congruent triangles (CPCTC)
(10) AB||DC //(9), Converse Alternate Interior Angles Theorem.
(11) ABCD is a parallelogram //(6), (10), definition of a parallelogram
