In addition to the standard formula for the area of a trapezoid using its bases, we can also calculate the area of a trapezoid with its median and its height. The median is the line connecting the two midpoints of the trapezoid’s legs – the non-parallel sides of a trapezoid. The median is also called the midsegment or midline.
Problem
BCD is a trapezoid, AB||CD. EF is a line connecting the midpoints of legs AD and BC, AE=ED and BF=FC. h is the height of the trapezoid. Find a formula for its area using h and |EF|
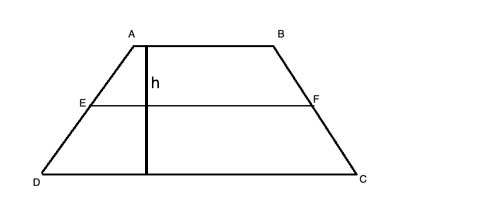
Strategy for Finding the Area of a Trapezoid with Median and Height
Let’s see how we can relate what we know about the trapezoid’s median to the formula we already have for the area of trapezoid. The area of a trapezoid is (short base+long base)·height/2, or A=½(AB+DC)·h.
In this problem, we have the height, and the median or midsegment. From the trapezoid midsegment theorem, we have the relationship between the midsegment and the bases: |EF|=½(AB+DC). Looking at the two formulas, we see we can simply substitute EF for ½(AB+DC) in the formula for the area and get A=|EF|·h
Solution
(1) A=½(AB+DC)·h //Area of trapezoid
(2) AE=ED, BF=FC //given
(3) EF is the midsegment //(2), Defintion of midsegment
(4) |EF| = ½(AB+DC) //(3), trapezoid midsegment theorem
(5) A = |EF| ·h //(1), (4), substitution
Another way to Solve this
In the above section, we relied on recognizing that the formula for the area of a trapezoid –A=½(AB+DC)·h looks very similar to the formula for the length of the midsegment – |EF| = ½(AB+DC) , and made a substitution that resulted in a very compact, elegant solution.
But what if we don’t immediately recognize that the formulas are similar, or don’t remember that the midsegment is equal to half the sum of the bases? Let’s look at another way to solve this, without relying on that.
Because EF is a line that connects midpoints of sides, we might be able to use the triangle midsegment theorem – but for that, we need a triangle. So let’s draw one, using the diagonal AC:
Solution using the triangle midsegment theorem
In triangle ΔACD, |EG| is a line parallel to the base CD, which starts from the midpoint of side AD – so by the converse triangle midsegment theorem, it is a midsegment, and equal to half the base. Let’s set |EG|=x. If x is equal to half the base, then the base CD must equal 2x.
Now let’s look at the other triangle, ΔACB. Using the same reasoning as above, |GF| starts from the midpoint of side BC and is parallel to AB – so by the converse triangle midsegment theorem, it is a midsegment, and equal to half the base. The length of |GF| is |EF|-x, so base AB is 2·(|EF|-x), or 2·|EF|-2x.
Now let’s plug those values into the formula for the area of a trapezoid:
(1) A=½(AB+CD)·h
(2) AB= 2·|EF|-2x
(3) CD=2x
(4) A=½(2·|EF|-2x+2x)·h = ½(2·|EF|)·h = |EF|·h
