The Trapezoid Midsegment Theorem states that a line segment connecting the midpoints of the legs of the trapezoid is parallel to the bases, and equal to half their sum.
Here, we'll prove the Converse of the Trapezoid Midsegment Theorem - a line that is parallel to the bases of a trapezoid and intersects the midpoint of one of the leg is a midsegment: It intersects the other leg's midpoint, and its length is equal to half the sum of lengths of the bases.
Problem
ABCD is a trapezoid. EF is a line segment parallel to its bases, AB and CD, and |AE|=|ED|. Show that EF is a midsegment in the trapezoid, that is, |BF|=|FC| and |EF|=½·(|AB|+|CD|)

Strategy
We've already proven a similar converse theorem for triangles, so let's try to use the triangle midsegment theorem. For that, we need a triangle - let's create one by drawing the diagonal AC, which intersects EF at point G.
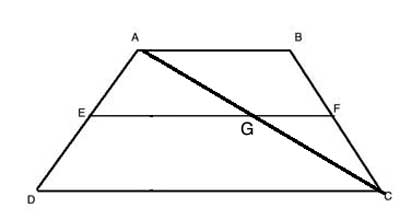
In triangle ΔACD, |EG| is a line parallel to the base CD, which starts from the midpoint of side AD – so by the converse triangle midsegment theorem, it is a midsegment. Because it is a midsegment, |AG|=|GC| and |EG| is equal to half the base. |EG| is then equal to half of CD: |EG|=½·|CD|
Now let’s look at triangle ΔACB. Using the same reasoning as above, because |AG|=|GC|, |FG| starts from the midpoint of side AC and is parallel to AB – so by the converse triangle midsegment theorem, it is a midsegment, and |BF|=|FC|, and we have proven the first part of the converse theorem
Proof
But because |FG| is a midsegment, it is also equal to half the base, so |FG|=½·|AB|. Now, |EF|=|EG|+|FG|= ½·|CD|+½·|AB|=½·(|AB|+|CD|), and we have proven the second part.
(1) EG || CD //Given
(2) |AE|=|ED| //Given
(3) EG is a midsegment in ΔACD //(1), (2), converse triangle midsegment theorem
(4) |AG|=|GC| //(3) , defintion of a triangle midsegment
(5) EG || AB //Given
(6) GF is a midsegment in ΔACB //(4), (5), converse triangle midsegment theorem
(7) |BF|=|FC| //(6) , defintion of a triangle midsegment
(8) |EG|=½·|CD| //(3), triangle midsegment theorem
(9) |GF|=½·|AB| //(6), triangle midsegment theorem
(10) |EF|=|EG|+|FG|= ½·|CD|+½·|AB|=½·(|AB|+|CD|)
