In today's geometry lesson, we will prove the trapezoid midsegment theorem, relying on the previously proven triangle midsegment theorem.
The triangle midsegment theorem states that the line connecting the midpoints of two sides of a triangle, called the midsegment, is parallel to the third side, and its length is equal to half the length of the third side.
There is a similar theorem for trapezoids: a line connecting the midpoints of the two legs of a trapezoid is parallel to the bases, and its length is equal to half the sum of lengths of the bases.
Problem
ABCD is a trapezoid, AB||CD. EF is a line connecting the midpoints of legs AD and BC, AE=ED and BF=FC. Prove that EF||DC and that EF=½(AB+DC)
Strategy
As we are dealing with the midpoints of segments, we will use what we have already proven for triangle midsegments. Let's create such triangles, by drawing a line from the vertex A through the midpoint, F, until it intersects an extension of the base DC at point G:
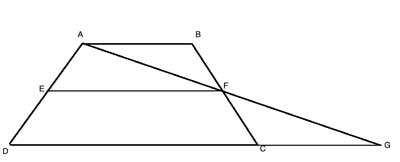
We can easily show that ΔABF and ΔGCF are congruent, using the Angle-Side-Angle postulate. From this, we can show that EF is a midsegment of triangle ΔADG. As such, by the Triangle midsegment theorem, it is parallel to DG and is equal to half of DG.
But DG is DC+CG, and as ΔABF and ΔGCF are congruent, CG=AB, so EF is equal to half of DC+AB. In other words, the length of EF is the arithmetic mean (average) of the lengths of the bases.
Proof
Here's how to prove the trapezoid midsegment theorem:
(1) AB||DG //Given, ABCD is a trapezoid
(2) ∠BAF ≅ ∠CGF // Alternate Interior Angles Theorem
(3)∠AED ≅ ∠CEF // Vertical angles
(4) BF=FC //Given
(5)ΔABF ≅ ΔGCF // (2), (3), (4), Angle-Side-Angle
(6) AF=FG //(5), corresponding sides of congruent triangles
(7) EF is midsegment //(6), definition of midsegment
(8) EF||DG //(7), Triangle midsegment theorem
(9)EF=½DG //(7), Triangle midsegment theorem
(10) DG = DC+CG
(11) CG=AB //(5), corresponding sides of congruent triangles
(12)EF=½(DC+CG) //(9), (10) , Transitive property of equality
(13) EF=½(DC+AB) //(11), (12) , Transitive property of equality
The converse of this theorem is also true - a line that is parallel to one of the trapezoid's bases and intersects one of the leg's midpoint also intersects the other leg's midpoint, and its length is equal to half the sum of the lengths of the bases.