In today's lesson, we will prove the Triangle Midsegment Theorem.
The midsegment of a triangle is a line that connects the midpoints of two of the sides:
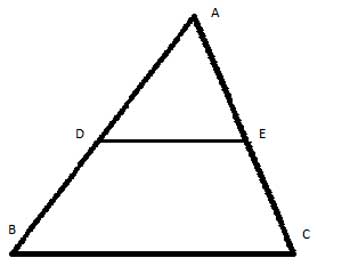
The Triangle Midsegment Theorem states that the midsegment is parallel to the third side, and its length is equal to half the length of the third side. We will now prove this theorem, as well as a couple of other related ones, and their converse theorems, as well.
Problem
Show that in triangle ΔABC, the midsegment DE is parallel to the third side, and its length is equal to half the length of the third side.
Strategy
To show that line segment lengths are equal, we typically use triangle congruency, so we will need to construct a couple of triangles here.
To show the congruency, we will need to rely on what is given in the problem statement, and see which parts (sides or angles) we know are equal. In this case, since DE is the midsegment, we know that AE=EC and AD=DB, so we should use one or more of these sides in the triangles we construct.
We also need to prove something about DE - that is is equal to half of BC - so it would be useful for the triangle we construct to have DE as a side, too, with another side equal to it - which we could construct. With that in mind, let's construct a new triangle by extending line DE to point F, so that DE=EF, and connecting F with C:
Now it is easy to show the new triangle we constructed (ΔCFE) is congruent to ΔADE using the Side-Angle-Side postulate, and as a result, that DFCB is a parallelogram since we now have two sides, DB and FC that are both equal and parallel.
And because DFCB is a parallelogram, DE is parallel to BC, as we needed to prove. From the congruency of ΔCFE and ΔADE, we also have DE=EF, and since DF= BC as opposite sides in a parallelogram, DE is half of BC.
Proof
(1) DE=EF //Construction
(2) AE=EC //Given, DE is a midsegment
(3) ∠AED ≅ ∠CEF // Vertical angles
(4) ΔADE ≅ΔCFE // Side-Angle-Side postulate
(5) ∠DAE ≅ ∠FCE // corresponding angles in congruent triangles, (CPCTC)
(6) AB||CF // Converse Alternate Interior Angles Theorem
(7) AD=CF // corresponding sides in congruent triangles, (CPCTC)
(8) AD=DB //Given, DE is a midsegment
(9) CF=DB //(7), (8), the transitive property of equality
(10) DFCB is a parallelogram //two opposite sides of a parallelogram, CF & DB, are equal and parallel
(11) DE||BC //(10), opposite sides of a parallelogram
(12) DF=BC //(10), opposite sides of a parallelogram
(13) DE=EF //(4) corresponding sides in congruent triangles, (CPCTC)
(14) DE= ½DF
(15) DE= ½BC //(12) , (14), substitution