The median of a triangle is a line drawn from one of the vertices to the mid-point of the opposite side. In the case of a right triangle, the length of the median to the hypotenuse is half the length of the hypotenuse, as we'll show in this proof.
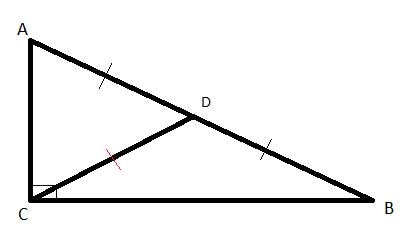
Problem
In the right triangle ΔABC, line segment CD is the median to the hypotenuse AB. Show that AD=DC; BD=DC
Strategy
As we need to show that a couple of line segments are equal (AD=DC; BD=DC) the tool we'll use is triangle congruency.
It might be tempting to try to use the existing triangles created by the median (ΔACD, ΔDCB), but a quick look at the drawing shows us that can't be right. And while it is never a good idea to rely on the drawing to make conclusions, we can imagine a right triangle that looks like this :

in which the two triangles can't possibly be congruent.
So we will need to construct new triangles in which the segments we want to prove are equal are corresponding sides.
Let's construct such triangles, by connecting point D (the midpoint of the hypotenuse) with the middle point of CB. This will have the advantage of creating two triangles where the segments we want to prove are equal are corresponding sides and having two sides we know are equal (CE and EB, as E is the midpoint).
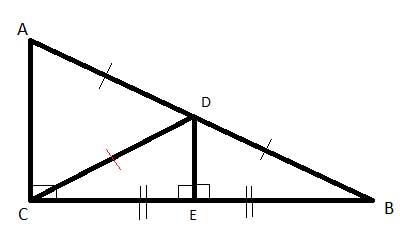
Now, D is the midpoint of the hypotenuse, and E is the midpoint of the leg CB, so DE is a midsegment, and using the triangle midsegment theorem, we know DE||AC. From this, we know ∠DEB ≅ ∠ACE (as corresponding angles) and they are both right angles. So m∠DEC=90°, too, as it forms a linear pair with ∠DEB.
And we can now prove the triangles ΔDCE and ΔDBE are congruent using the Side-Angle-Side postulate, with the result that CD=DB as the corresponding sides, just as we need to show.
As a result, we also see that the median to the hypotenuse creates two isosceles triangles, ΔDCB and ΔDAC, where DA=DC=DB.
Proof
(1) AD=DB //given, CD is the median to the hypotenuse
(2) CE=EB //construction
(3) DE is a midsegment //(1), (2) , Definition of a midsegment
(4) DE||AC //triangle midsegment theorem
(5) ∠DEB ≅ ∠ACE // corresponding angles in two parallel lines intersected by a transversal line (CE)
(6) m∠ACE=90° //given, ΔABC is a right triangle
(7) m∠DEB=90° //(5), (6), definition of congruent angles
(8) m∠DEC=180° - 90° = 90° // linear pair
(9) ∠DEB ≅ ∠DEC //(7),(8), definition of congruent angles
(10) DE=DE //common side, reflexive property of equality
(11) ΔDCE ≅ ΔDBE //(2), (9), (10) Side-Angle-Side postulate
(12) CD=DB // Corresponding sides in congruent triangles (CPCTC)
(13) DB= ½AB // Given, CD is the median to the hypotenuse
(14) CD= ½AB //(12) , (13), substitution
Another way to prove this
One of the fun things about these proof problems is that often there is more than one way to approach and prove the theorem. And indeed, one of my regular readers sent me the following solution, which is quite elegant, and does not rely at all on the midsegment theorem. Instead, it uses angle construction and some simple angle math to show that the median creates two isosceles triangles.
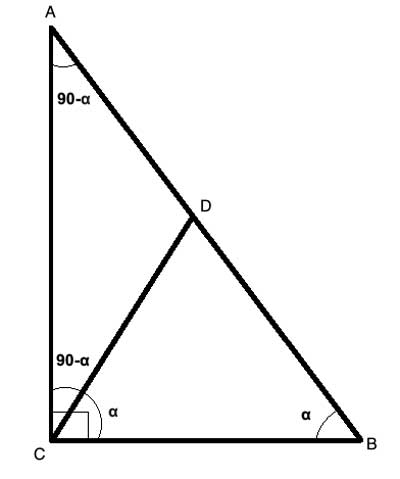
In right triangle ΔABC, let's construct a line CD, that splits the right angle ∠ACB into 2 angles, ∠ACD and ∠DCB, such that ∠DCB≅∠DBC, and call that angle α. Since we constructed ∠DCB≅∠DBC, by the converse base angles theorem, ΔDCB is isosceles and |DC|=|DB|.
Now let's do some angle math. If ∠DBC=α, and m∠ACB=90°, then by the sum of angles in a triangle theorem, m∠BAC=90°-α. And since m∠ACB=90° and we constructed ∠DCB≅∠DBC=α, then m∠ACD=90°-α. So m∠ACD=m∠BAC=90°-α, and ΔDCB is also an isosceles triangle and |DC|=|DA|. Using the transitive property of equality, if |DC|=|DB| and |DC|=|DA|, then |DB|=|DA|.
But if |DB|=|DA|, then by definition CD is the median to the hypotenuse. And |CD| it is equal to half of |AB| it since it is one of the equal legs in both the isosceles triangles we created!
Nice and simple - thanks, Ben!
Converse Theorem
Now let's prove the converse theorem: If the median to a side is equal to half that side, then the triangle is a right triangle. As always with converse theorems, we'll use a very similar strategy to the one used in proving the theorem, reversing what is given and what is needed to prove.
If the median to the side is equal to half the side, then CD=DB=DA. We'll draw a perpendicualr line from D, to the base BC. Now we have m∠DEB = m∠DEC = 90° since we constructed DE as perpendicualr to BC and ∠DEB and ∠DEC are a linear pair. DE=DE as a common side, so triangles ΔDCE and ΔDBE are congruent using the hypotenuse-leg postulate, with the result that CE=EB as corresponding sides.
But if CE=EB, and DB=DA, then DE is a midsegment in triangle ΔABC, by defintion. And form the triangle midsegment theorem , DE||AC . Then, ∠DEB ≅ ∠ACE as corresponding angles in two parallel lines intersected by a transversal line (CE). And as m∠DEB = 90°, m∠ACB = 90°, and triangle ΔABC is a right triangle.
