In today’s lesson, we will prove the converse to the Base Angle theorem – if two angles of a triangle are congruent, the triangle is isosceles. We will use congruent triangles for the proof.
From the definition of an isosceles triangle as one in which two sides are equal, we proved the Base Angles Theorem – the angles between the equal sides and the base are congruent.
Now we’ll prove the converse theorem – if two angles in a triangle are congruent, the triangle is isosceles.
Problem
In triangle ΔABC, the angles ∠ACB and ∠ABC are congruent. Prove that ΔABC is isosceles, i.e. that AB=AC.
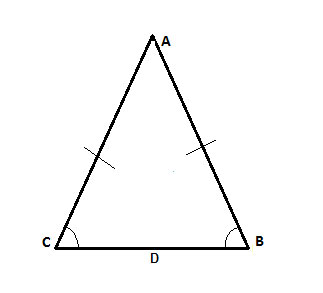
Strategy
When proving the Converse Base Angle theorem, we will do what we usually do with converse theorems. We will try to apply the same strategy we used to prove the original one – the Base Angles Theorem.
There, we drew a line from A to the base BC and proved the resulting triangles are congruent. As a result, the base angles were congruent.
We’ll do the same here, prove the triangles are congruent relying on the fact that the base angles are congruent. And as a result, the corresponding sides, AB and AC, will be equal.
And just like in the original theorem, we have a choice of which line to draw. We can draw either the altitude to the base, and use the fact that it creates a linear pair of equal right angles. Or, draw the angle bisector of A, and use the fact that it creates a pair of equal angles at A.
In today’s lesson on proving the Converse Base Angle Theorem, we’ll provide a proof for both.
Proof
First, we’ll draw AD, the height to the base:
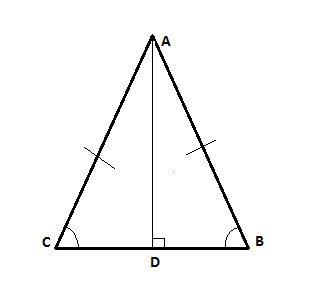
(1) ∠ACB ≅ ∠ABC //Given
(2) AD = AD // Common side to both triangles, reflexive property of equality
(3) m∠ADC= m∠ADB=90° //construction
(4) ∠ADC≅∠ADB //(3), definition of congruent angles
(5) △ABD≅△ACD //(1), (4), (3), Angle-Angle-Side postulate
(6) AB = AC // Corresponding sides in congruent triangles (CPCTC)
Now let’s repeat it, using AD, the angle bisector:
(1) ∠ACB ≅ ∠ABC //Given
(2) AD = AD // Common side to both triangles, reflexive property of equality
(3) ∠CAD≅∠BAD // Given, AD is the bisector
(5) △ABD≅△ACD //(1), (3), (2), Angle-Angle-Side postulate
(6) AB = AC // Corresponding sides in congruent triangles (CPCTC)
