Today's geometry problem presents an application of the angle bisector theorem in a triangle. It also incorporates several other concepts we've explored, like the properties of isosceles triangles and congruent triangles.
This is a more challenging problem, so don't give up too quickly! It's completely doable if you follow the steps slowly and methodically.
Problem
In triangle △ABC, AE is the angle bisector of ∠BAC (∠BAE≅∠CAE). G is the midpoint of side AB (AG=GB) and H is the midpoint of side AC (AH=HC). Also, FG=AH. FE is perpendicular to AE. Show that BD=DC.
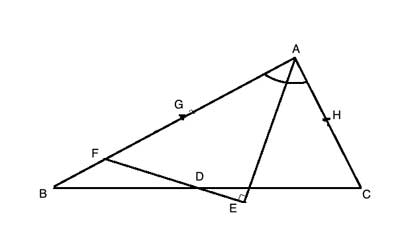
Strategy
Since we are given two midpoints of sides in a triangle, it is tempting to try and use the triangle midsegment theorem. Especially since the theorem says the length of the midsegment is half of the base - so perhaps we might be able to show that GH is equal to either BD or DC, and have our proof.
Indeed, I tried to solve this problem that way, but got nowhere. Perhaps it is possible, but I haven't figured out how, yet.
So let's try a different way- using the fact that we have an angle bisector. AE is both the angle bisector of ∠BAC, and perpendicular to FE. Recall that in an isosceles triangle, the height to the base bisects the apex angle.
And the converse of this is also true - If the bisector of an angle in a triangle is perpendicular to the opposite side, the triangle is isosceles.
Thus, if we extend FE and AC until they intersect at point J, we will have a triangle (△AFJ). And by the above converse theorem, it is an isosceles triangle, in which AF=AJ.
Now let's do some side length math: H is the midpoint of side AC, so we'll label the two equal halves (AH and HC) 'x'. FG is equal to AH, so we will label it 'x', too, and we'll label each half of AB 'y'. G is the midpoint of side AB, so AG=GB=y, so FB which is GB-GF, is y-x.
On the other side, AB=2x, and since △AFJ is isosceles, AJ=AF, and AJ=x+y. AJ is 2x+CJ, so y+x=2x+CJ. CJ is thus y-x, and equal to FB .
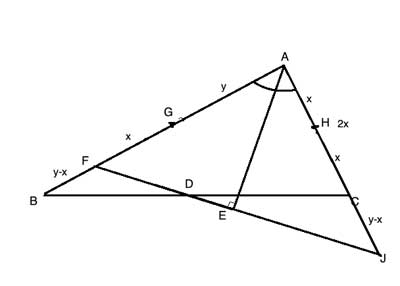
This is good progress - we now have two equal sides (CJ=FB) and a pair of equal angles (the two vertical angles at point D). But triangles △BFD and △CJD are clearly not congruent. In an isosceles triangle (△AFJ), the hight to the base bisects the base, so FE=EJ. And that means that FD, which is a smaller part of FE, can't be equal to DJ.
So what we need to do is to construct some triangles where CE and EB would be sides and the vertical angles at D would be interior angles, and then find some other equal side or angle. If we had that, we could use one of the congruent triangle postulates.
This is the tricky part. After some experimenting, we come up with the following idea: draw a line, CK, that is parallel to AB. Because CK||AB, ∠AFE≅∠CKJ, as corresponding angles of two parallel lines. But since △AFJ is isosceles, ∠AFE≅∠CJK, as base angles. So ∠CKJ≅∠CJK, and triangle △AFJ is isosceles by the converse base angle theorem.
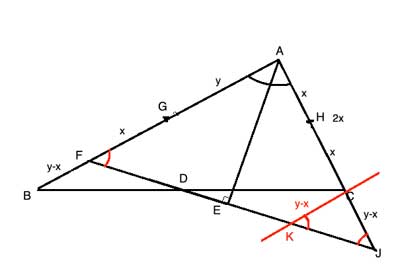
From this we get CJ=CK, so FB=CK. And, because CK||AB, ∠FBD≅∠DCK, as alternating interior angles, and also ∠BFD≅∠CKD as alternating interior angles. We can now prove △BFD is congruent to △CKD, and BD=DC as corresponding sides.
Proof
(1) ∠BAE≅∠CAE //Given
(2) AE⊥FE // Given
(3) △AFJ is isosceles // Angle bisector is perpendicular to opposite side → isosceles triangle
(4) AF=AJ // Definition of isosceles trinangle
(5) AH=HC=x // Given
(6) FG=AH=x // Given
(7) AG=GB=y // Given
(8) FB = GB-GF=y-x //(6), (7)
(9) AJ=AH+HC+CJ=2x+CJ //(5)
(10) AF=x+y=AJ //(4)
(11) x+y=2x+CJ /(9), (10)
(12) CJ=y-x //Simplify (11)
(13) CJ=FB //(8), (12)
(14) CK||AB //Construction
(15) ∠AFE≅∠CKJ //Corresponding angles of two parallel lines
(16) ∠AFE≅∠CJK // Base angles theorem
(17) ∠CKJ≅∠CJK //(15), (16), Transitive property of equality
(18) CJ=CK // converse base angle theorem
(19) FB=CK //(13), (18), Transitive property of equality
(20) ∠FBD≅∠DCK //(14), alternating interior angles
(21) ∠BFD≅∠CKD //(14), alternating interior angles
(22) △BFD≅ △CKD //(19),(20),(21), Angle-side-Angle postulate
(23) BD=DC // Corresponding sides in congruent triangles (CPCTC)
So you see that we used the angle bisector theorem in a triangle to solve a truly difficult geometry problem, and survived! 🙂