In today's lesson we'll learn a simple strategy for proving that in an isosceles triangle, the height to the base bisects the base.
Having proven the Base Angles Theorem for isosceles triangles using triangle congruency, we know that in an isosceles triangle the legs are equal and the base angles are congruent.
With these two facts in hand, it will be easy to show several other properties of isosceles triangles using the same method (triangle congruency).
Let's start by proving that in an isosceles triangle, the height (or altitude) to the base bisects the base.
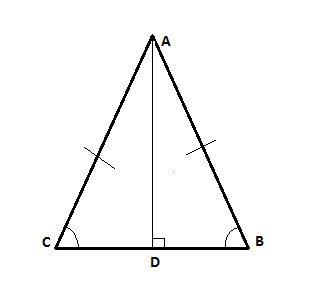
Problem
Prove that in isosceles triangle ΔABC, the height to the base, AD, bisects the base.
Strategy
The strategy for this and for the remaining similar problems (showing that the altitude to the base bisects the apex angle, showing that the angle bisector is perpendicular to the base, etc...) will be the same.
We already have a pair of equal edges (the legs, per the definition of an isosceles triangle) and a pair of congruent angles (per the Base Angles Theorem). So we will find or construct another pair of congruent angles or another pair of equal sides, and use one of the triangle congruency postulates to show the two triangles are congruent.
So here, we know that AD is the height to the base. By definition, that means that the angle it creates with the base (∠ADB) is a right angle. And, so is ∠ADC, and we have our second pair of congruent angles.
Proof
(1) ΔABC is isosceles // Given
(2) AB=AC // Definition of an isosceles triangle
(3) ∠ACB ≅ ∠ABC // Base angles theorem
(4) m∠ADB =m∠ADC = 90° // Definition of height to base
(5) △ABD≅△ACD // angle-angle-side
(6) BD=DC // Corresponding sides in congruent triangles (CPCTC)
