In today's lesson, we will prove the Converse Angle Bisector Theorem for Isosceles Triangles. We'll show that if a triangle's angle bisector is perpendicular to the opposite side, the triangle is an isosceles triangle.
One of the properties of an isosceles triangle is that the height to the base bisects the apex angle.
The converse of this is also true - If the bisector of an angle in a triangle is perpendicular to the opposite side, the triangle is isosceles.
Problem
In triangle △ABC, the bisector of angle ∠BAC is perpendicular to the base BC. Prove that △ABC is an isosceles triangle.
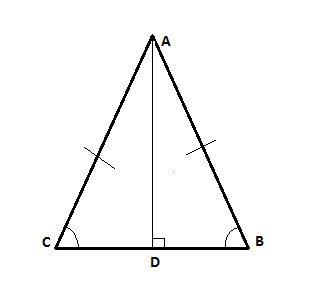
Strategy
As with most converse theorems, we will simply take the proof of the original theory, and use the same strategy (congruent triangles).
We have one common side (AD). We have one pair of congruent angles formed by the angle bisector. AD is the height to the base, which by definition means that the angle it creates with the base (∠ADB) is a right angle, and so is ∠ADC.
So ∠ADB is congruent to ∠ADC and we have our second pair of congruent angles. We can now show that the triangles are congruent. And as a result, AB=AC and the triangle is isosceles.
Proof
(1) ∠BAD ≅ ∠CAD //Given, AD is the angle bisector
(2) AD=AD // Common side, reflexive property of equality
(3) m∠ADB =m∠ADC = 90° // Definition of height to base
(4) ∠ADB ≅∠ADC //(3), definition of congruent angles
(5) △ABD≅△ACD // angle-side-angle
(6) AB=AC // Corresponding sides in congruent triangles (CPCTC)
(7) ΔABC is isosceles //(6), definition of isosceles triangle