In today's lesson, we will prove the converse of the scalene triangle inequality. Using proof by contradiction, we will show that the side facing the larger angle is longer.
Having proven the Scalene Triangle Inequality- that if in a scalene triangle ΔABC, AB>AC then m∠ACB> m∠ABC - proving the converse is very simple.
Problem
In scalene triangle ΔABC, m∠ACB> m∠ABC. Show that AB>AC.
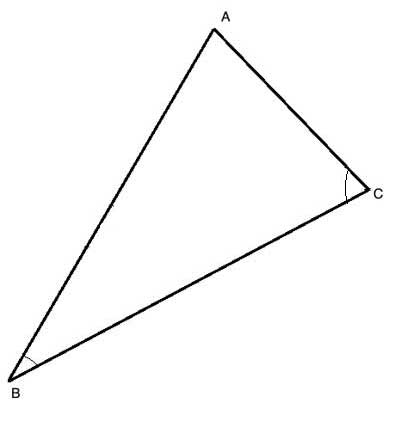
Strategy
When proving converse theorems, it is often useful to use proof by contradiction. What do I mean when I say "proof by contradiction?" I mean we should assume that the converse theorem is NOT true.
Then we will see that in combination with the original theorem (which we know IS true), it leads to a contradiction.
That means the original assumption (that the converse is NOT true) is incorrect. And this is exactly what we will do here.
First assume that AC>AB. By the Scalene Triangle Inequality, we know that if AC>AB, then m∠ABC> m∠ACB. This contradicts what we were given - that m∠ACB> m∠ABC. So AC cannot be larger than AB.
Similarly, if we assume that AC=AB, then by the Base Angle Theorem, m∠ABC= m∠ACB, which contradicts what we were given - m∠ACB> m∠ABC. So AC cannot be equal to AB.
So if AC cannot be larger or equal to AB, it must be smaller. And thus we have proved the converse of the Scalene Triangle Inequality.
