Let's say you have a pair of triangles with two congruent sides but a different angle between those sides. Think of it as a hinge, with fixed sides, that can be opened to different angles:
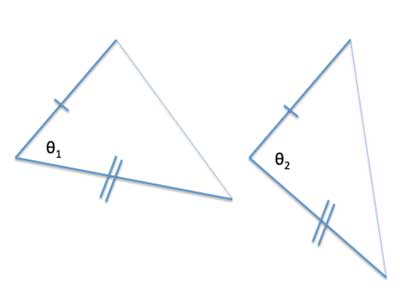
The Hinge Theorem states that in the triangle where the included angle is larger, the side opposite this angle will be larger.
It is also sometimes called the "Alligator Theorem" because you can think of the sides as the (fixed length) jaws of an alligator- the wider it opens its mouth, the bigger the prey it can fit.
We'll prove this theorem two ways.
Problem
Two triangles, △ABC and △DEF, have two pairs of congruent sides: |AB|=|DE|; |BC|=|EF|. θ2=∠DEF>∠ABC=θ1. Show that |DF|>|AC|
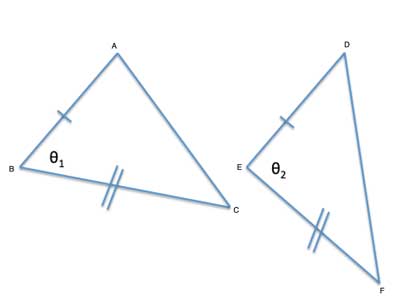
Strategy
To prove this Theorem, we need to show that one line segment is larger than another. Both lines are also sides in a triangle. This guides us to use one of the triangle inequalities which provide a relationship between sides of a triangle. One of these is the converse of the scalene triangle Inequality.
This tells us that the side facing the larger angle is larger than the side facing the smaller angle. The other is the triangle inequality theorem, which tells us the sum of any two sides of a triangle is larger than the third side.
We'll use each one of these in the two different ways we prove the Theorem.
But one hurdle first: both these theorems deal with sides (or angles) of a single triangle. Here we have two separate triangles. So the first order of business is to get these sides into one triangle.
Let's place triangle △ABC over △DEF so that one of the congruent edges overlaps, and since θ2>θ1, the other congruent edge will be outside △ABC:
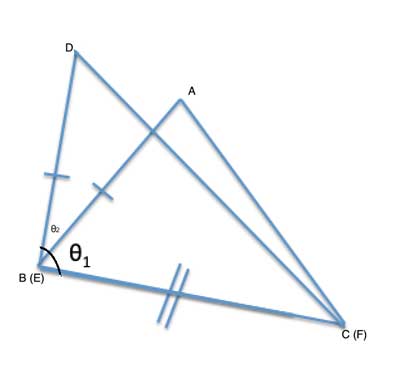
The above description was a colloquial, layman's description of what we are doing. In practice, we will use a compass and straight edge to construct a new triangle, △GBC, by copying angle θ2 into a new angle ∠GBC, and copying the length of DE onto the ray BG so that |DE=|GB|=|AB|.
We'll now compare the newly constructed triangle △GBC to △DEF. We have |DE=|GB| by construction, θ2=∠DEF=∠GBC by construction, and |BC|=|EF| (given). So the two triangles are congruent by the Side-Angle-Side postulate, and as a result |GC|=|DF|.

First method - using the converse scalene triangle inequality
Let's look at the first method for proving the Hinge Theorem. To put the edges that we want to compare in a single triangle, we'll draw a line from G to A. This forms a new triangle, △GAC. This triangle has side AC, and from the above congruent triangles, side |GC|=|DF|.
Now let's look at △GBA. |GB|=|AB| by construction, so △GBA is isosceles. From the Base Angles theorem, we have ∠BGA= ∠BAG. From the angle addition postulate, ∠BGA>∠CGA, and also ∠CAG>∠BAG. So ∠CAG>∠BAG=∠BGA>∠CGA, and so ∠CAG>∠CGA.
And now, from the converse of the scalene triangle Inequality, the side opposite the large angle (GC) is larger than the one opposite the smaller angle (AC). |GC|>|AC|, and since |GC|=|DF|, |DF|>|AC|
Second method - using the triangle inequality
For the second method of proving the Hinge Theorem, we'll construct the same new triangle, △GBC, as before. But now, instead of connecting G to A, we'll draw the angle bisector of ∠GBA, and extend it until it intersects CG at point H:
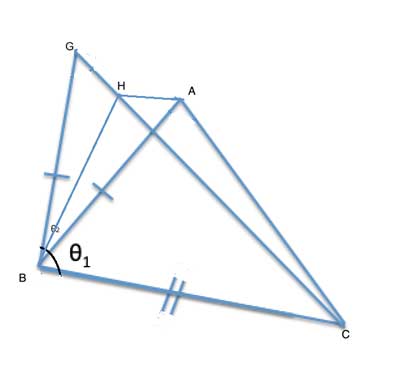
Triangles △BHG and △BHA are congruent by the Side-Angle-Side postulate: AH is a common side, |GB|=|AB| by construction and ∠HBG≅∠HBA, since BH is the angle bisector. This means that |GH|=|HA| as corresponding sides in congruent triangles.
Now consider triangle △AHC. From the triangle inequality theorem, we have |CH|+|HA|>|AC|. But as |GH|=|HA|, we can substitute and get |CH|+|GH|>|AC|. But |CH|+|GH| is simply |CG|, so |CG|>|AC|, and as |GC|=|DF|, we get |DF|>|AC|
And so we were able to prove the Hinge Theorem in two ways, relying on the triangle inequality theorem or its converse.
