We all know that “the shortest distance between two points is a straight line.” That is the informal way of describing the Triangle Inequality Theorem.
If we want to go from point A to point B, getting there through any intermediate point C, which is not on the straight line between A and B, is going to be longer. This should seem intuitively correct. But we will prove it formally.
Where do triangles come into this? Imagine that the line AB is a side of a triangle, ΔABC. Going from A to B is the straight, short way. Going there by first going to another point, C (which is the side AC) and then from C to B (which is the side CB) is going to be longer.
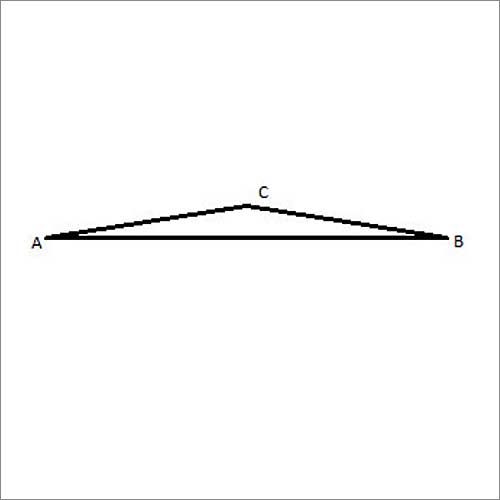
Problem
In a triangle ΔABC, show that AB+AC> BC, AB+BC>AC and AC+CB>AB
Strategy for proving the Triangle Inequality Theorem
We have already proven that the shortest distance between a point P, and a line, l, is the perpendicular line from P to l.
This problem sounds similar, so we will try to use that shortest distance theorem. To do that, we need a perpendicular line, so let’s draw it:
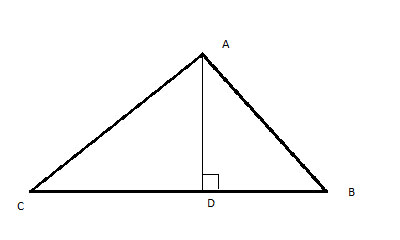
This looks really similar to:
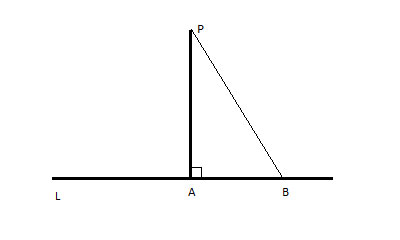
So we can immediately see that AB>BD, and also that AC>CD.
So if we use the shortest distance theorem twice, for the two triangles created by drawing the height, we will have our proof.
Proof
(1) AD ⊥ BC //given, we constructed AD as the height from A to BC
(2) AB > BD //shortest distance theorem
(3) AC > CD //shortest distance theorem
(4) AB+AC > BD+CD //Add (2) and (3)
(5) BD+CD = BC //given
(6) AB+AC>BC //substitute (5) into (4)
And we can repeat this process, drawing the height from B to AC, and from C to AB to prove the other two statements.
