Today we will prove one of the properties of deltoids. We will show that one of the diagonals in deltoids bisects the angles at its endpoints.
A deltoid is a quadrilateral with one axis of symmetry. The diagonal that connects the two corners formed by the sides that are equal creates this axis of symmetry.
So we can "fold" the deltoid over this line of symmetry and the two parts will match - meaning that this diagonal also bisects the angles at its endpoints, as we will now prove.
Problem
In a deltoid ABCD, show that the diagonal forming the axis of symmetry bisects the angles at its endpoints.
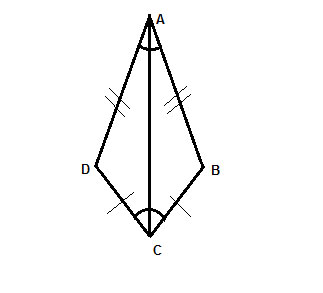
Show that ∠BAC ≅ ∠DAC and that ∠BCA ≅ ∠DCA
Strategy
As in other similar problems, to show that angles are equal when we have no parallel lines, we will use triangle congruence.
Another hint is that we need to show that the angles are bisected, we know a deltoid is made up of two isosceles triangles, and we have proven that in an isosceles triangle the height to the base bisects the apex angle using a very similar technique.
And in this case, since deltoids are by definition made up of two pairs of equal sides, we are clearly directed to use the Side-Side-Side postulate.
Proof
(1) ABCD is a deltoid //Given
(2) AB=AD //definition of deltoid
(3) BC=CD //definition of deltoid
(4) AC=AC //Common side
(5) △ABC≅△ADC //Side-Side-Side postulate.
(6) ∠BAC ≅ ∠DAC //Corresponding angles in congruent triangles (CPCTC)
(7) ∠BCA ≅ ∠DCA //Corresponding angles in congruent triangles (CPCTC)
