A Rhombus has two axes of symmetry, created by the diagonals. Since it is symmetrical, the diagonals bisect the angles, as we will show using triangle congruence.
Problem
In a rhombus ABCD, prove that the diagonals bisect the angles.
i.e prove that ∠BAC ≅ ∠DAC and that ∠BCA ≅ ∠DCA; and also that ∠ADB ≅ ∠CDB and ∠ABD ≅ ∠CBD
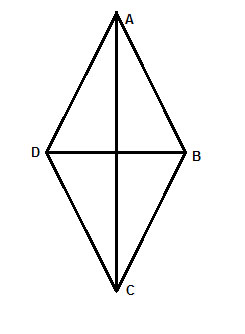
Strategy
Wow, that's a lot of angles and a lot of triangles!
Fortunately, we know so much about the sides, as we are dealing with a rhombus, where all the sides are equal.
We will use triangle congruence to show that the angles are equal, and rely on the Side-Side-Side postulate because we know all the sides of a rhombus are equal.
We will do this first for the angles ∠BAC ≅ ∠DAC and ∠BCA ≅ ∠DCA, following the exact same proof we did for a kite, and then we will repeat the process for the other two pairs of angles, using the other diagonal.
Proof
(1) ABCD is a rhombus //Given
(2) AB=AD //definition of rhombus
(3) BC=CD //definition of rhombus
(4) AC=AC //Common side
(5) △ABC≅△ADC //Side-Side-Side postulate.
(6) ∠BAC ≅ ∠DAC //Corresponding angles in congruent triangles (CPCTC)
(7) ∠BCA ≅ ∠DCA //Corresponding angles in congruent triangles (CPCTC)
This is just what we did for a kite. Now for the second part:
(1) AD=DC //definition of rhombus
(2) AB=BC //definition of rhombus
(3) DB=DB //Common side
(4) △ADB≅△CDB //Side-Side-Side postulate.
(5) ∠ADB ≅ ∠CDB //Corresponding angles in congruent triangles (CPCTC)
(6) ∠ABD ≅ ∠CBD //Corresponding angles in congruent triangles (CPCTC)
