The three parallel lines theorem is another theorem that provides a ratio between line segments created by a transversal of parallel lines, similar to the Intercept Theorem.
It states that if three lines that are all parallel to each other are intersected by two transversal lines, the line segments of the traversal lines that are cut by the parallel line have equal proportions:
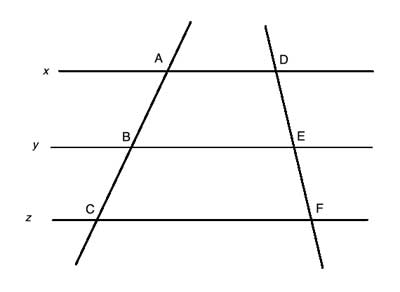
|AB|/|BC|=|DE|/|EF|
Problem
Two transversal lines intersect three parallel lines, x, y, and z, at points A,B,C and D, E,F respectively. Show that |AB|/|BC|=|DE|/|EF|
Strategy
This theorem is very similar to the Intercept Theorem, and the drawing looks very much like that of the intercept theorem:
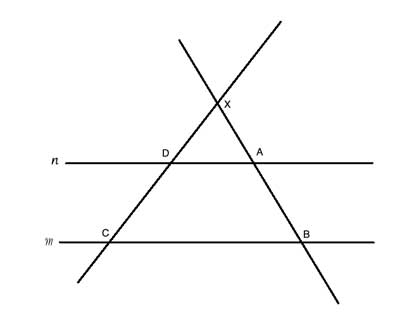
So let's see if we can use this theorem in our proof. We'll draw a line parallel to DF through point A (Remember the axiom: “for every straight line and every point not on that line, there is one straight line that passes through that point, parallel to the first line.”) :
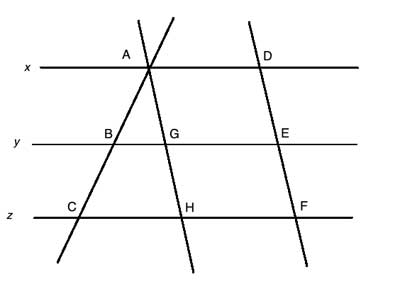
Now the left side of the drawing is exactly what we have in the intercept theorem. Using that, directly, we have |AB|/|BC|=|AG|/|GH|.
But as x,y, and z are all parallel, and AH is parallel to DF by construction, ADEG and GEFH are both parallelograms. And in a parallelogram, opposite sides are equal, so |AG|=|DE| and |GH|=|EF|. Substituting, we have the needed result: |AB|/|BC|=|AG|/|GH|=|DE|/|EF|
And this is how we prove the Three Parallel Lines Theorem.
Proof
(1) x || y || z //Given
(2) AH||DF //Construction
(3) |AB|/|BC|=|AG|/|GH| //Intercept theorem
(4) |AG|=|DE| //(1), (2), Opposite sides of a parallelogram are equal
(5) |GH|=|EF| //(1), (2), Opposite sides of a parallelogram are equal
(6) |AB|/|BC|=|DE|/|EF| //(3), (4), (5) , Transitive property of equality
Corollary
A corollary is a proposition that follows from a proof that we have just proved. A corollary to the three parallel lines theorem is that if three parallel lines cut off congruent segments on one transversal line, then they cut off congruent segments on every transversal of those three lines.
This corollary follows directly from what we have proven above. We have shown that when we have three parallel lines, the ratios of the segments cut off on the transversal lines are the same: |AB|/|BC|=|DE|/|EF|. It follows that if AB and BC are congruent, |AB|/|BC|=1, and so |DE|/|EF| = 1. And this is true for any transversal line with segments DE and EF cut off by the three parallels.
An interesting application of this corollary is that if you take a notebook that has ruled pages, and draw any straight line across the guidelines, the segments of that straight line cut off by the guidelines are all equal:
This is because the guidelines are equally spaced. So the distance between any two adjacent lines is the same. The distance is the length of a perpendicular line from one parallel line to another. For example, the red line in the left margin of the above drawing.
So any three adjacent lines have a ratio of |AB|/|BC|=1. And by the corollary above, the 3 parallel lines will cut off congruent segments on every transversal of those three lines.