The Intercept theorem provides the ratios between the line segments created when two parallel lines are intercepted by two intersecting lines.
It is sometimes called "Thales' Theorem" (not to be confused with another one of his theorems related to inscribed angles, also called Thales' Theorem) after the Greek mathematician to whom the proof is attributed.
Problem
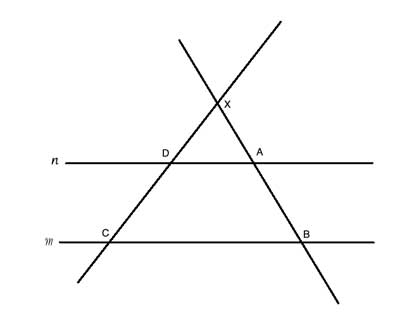
m and n are parallel lines. XC and XB are two intersecting lines that intercept m and n. Show that the following relationship between the lengths of the line segments is true:
XD/XC=XA/XB =DA/CB and XD/DC=XA/AB
Strategy
When proving the Intercept Theorem, we will use our go-to method when required to show equal ratios of two pairs lines- similar triangles.
Here, the similar triangles are obvious: △XDA is similar to △XCB, as both triangles share the apex angle X, and the other two pairs of angles are congruent as corresponding angles of two parallel lines formed by transversal lines.
The first ratio relationship (XD/XC=XA/XB =DA/CB) is a direct consequence of the triangle similarity since all the line segments involved are corresponding sides in similar triangles.
The second relationship (XD/DC=XA/AB) also follows from the triangle similarity, with a bit of algebra. Set XA=x; AB=y; XD=z; DC=w.
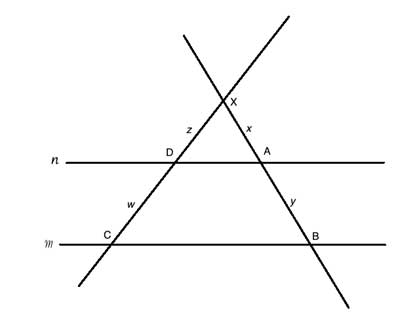
Then, from the triangle similarity, x/(x+y)=z/(z+w). Cross multiply to get x(z+w) = z(x+y).
Thus xz+xw=zx+zy, or xw =zy. rearrange to get x/y=z/w, and substitute back the line segments to get XA/AB=XD/DC
Proof
(1) ∠DXA≅∠CXB //Common angle, reflexive property of equality
(2) n || m // Given
(3) ∠XDA≅∠XCB //(2), Corresponding angles from by a transversal of parallel lines
(4) ∠XAD≅∠XBC //(2), Corresponding angles from by a transversal of parallel lines
(5) △XDA ∼ △XCB //(1) , (3) , (4) Angle-Angle-Angle
(6) XD/XC=XA/XB =DA/CB //(5), corresponding sides of similar triangles
Set XA=x; AB=y; XD=z; DC=w
(7) x/(x+y)=z/(z+w) //(5), corresponding sides of similar triangles
(8) xz+xw=zx+zy //(7) , cross-multiply
(9) xw = zy //(8), subtract xz from both sides, subtraction property of equality
(10) x/y=z/w //(9), divide both side by wy , division property of equality
(11) XA/AB=XD/DC //(10), substitute back XA=x; AB=y; XD=z; DC=w