In today's lesson, we will prove that the inscribed angle that subtends the diameter of a circle is always a right angle, using the sum of angles in a triangle.
Thales of Miletus was a Greek mathematician whose work predates that of Euclid and Pythagoras.
There are a number of theorems associated with his name. One is the Intercept Theorem for the ratios between the line segments created when two parallel lines are intercepted by two intersecting lines, and here we'll prove another one, related to inscribed angles.
The theorem states that any inscribed angle in a circle that subtends the diameter is a right angle.
Problem
CB is the diameter of a circle with center O, and A is a point on the circle's circumference. Show that m∠CAB=90°
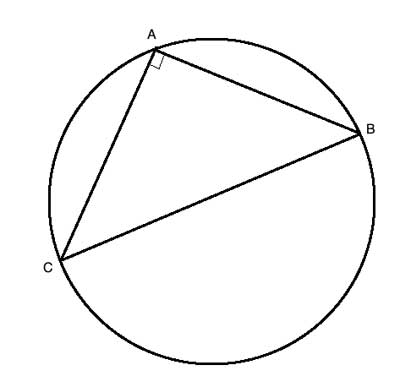
Strategy
One way to prove this is to treat it as a special case of the inscribed angle theorem: The central angle is equal to twice the inscribed angle which subtends the same arc; the diameter splits a circle (which by definition is 360°) into two equal halves, so its central Anglo measure is 180°, and the inscribed angle which subtends it must be half that, or 90°.
But as Thales' work predates Euclid's (who proved the general theorem for inscribed angles), let's prove it directly, without relying on the inscribed angle theorem.
Connect the center O to point A. OA is a radius, and so are OB and OC. All radii are equal, so the two triangles we created - ΔOAC and ΔOAB - are both isosceles triangles. And, by the base angle theorem, their base angles are equal. Let's label the base angles of ΔOAB 'α', and those of ΔOAC 'β'.
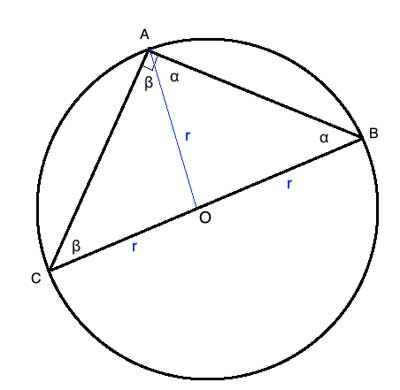
The sum of angles in a triangle is 180°. So α+α+β+β= 180°, 2*(α+β)= 180° so α+β=90°. And since ∠CAB = α+β, it is a right angle.
Proof
(1) OA=OB=OC=r //all radii are equal
(2) ∠OCA≅∠OAC=β //Base angle theorem
(3) ∠OBA≅∠OAB=α //Base angle theorem
(4) α+α+β+β= 180° //sum of angles in a triangle
(5) 2*(α+β)= 180° //(4), distributive property of multiplication
(6) α+β=90° //(5), divide by 2
(7) ∠CAB = mα+β //angle addition postulate
(8) m∠CAB=90°
