A regular polygon is one in which all angles are equal and all sides are equal. So by definition, all regular polygons with the same number of sides are similar to each other.
An equilateral triangle is a regular polygon with 3 sides, so all equilateral triangles are similar. We will use this in the following geometry problem.
Problem
△ABC and △BDE are both equilateral triangles. BE=EC. Show that the area of △BDF is twice the area of △DFE.

Strategy
In a previous similar problem, we noted that problems that require finding the ratio of areas often rely on using similar triangles, or on triangles that have the same base or same height.
Here, the triangles whose areas we are asked to compare (△BDF and △DFE) have the same height, DG, so their areas will be proportional to the length of their bases, BF and FE. What need to show then is that BF=2FE.
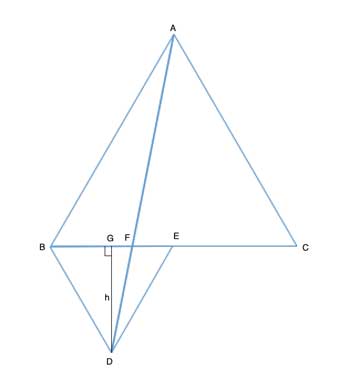
To show that BF=2FE, we will use similar triangles, and the hint we have is that we already have two line segments with that ratio: BE=EC, so BC=2BE. △ABC and △BDE are both equilateral triangles, so they are similar triangles, and the scale factor is 1:2.
Now let's look at two triangles where FE and BF are sides - △ABF and △DEF. m∠ABF=m∠DEF=60°, since △ABC and △BDE are both equilateral triangles. ∠AFB ≅ ∠DFE because they are vertical angles. So △ABF and △DEF are similar triangles and AB/ED=BF/FE.
But the ratio AB/ED is the same as BC/BE, because △ABC and △BDE are similar triangles with a scale factor of 1:2, so AB/ED=2/1=BF/FE, and we have shown that BF=2FE. As a result, the area of △BDF is twice the area of △DFE.
Proof
(1) △ABC ∼ △BDE //All equilateral triangles are similar
(2) BE=EC //Given
(3) BC=2BE //(2)
(4) AB=2ED //(3), (1) , scale factor of similar triangles
(5) m∠ABF=m∠DEF=60° //All angles of equilateral triangles measure 60°
(6) ∠AFB ≅ ∠DFE //vertical angles
(7) △ABF ∼ △DEF //(5),(6), Angle-Angle
(8) AB/ED=BF/FE //(7), similar triangles
(9) BF/FE = 2 //(4),(8)
(10) AreaBDF/AreaDFE=2 //triangles with same height have areas proportional to their bases
