Ratio of Area of Triangles in a Trapezoid

In today's lesson, we will use similar triangles and triangles with the same height to find the ratio between areas of triangles formed by the intersection of a trapezoid's diagonals.

The diagonals of a trapezoid form 2 similar triangles. and two other sets of triangles that share the same base and height. This property is used in many geometry problems that require you to find the ratio of the areas of those triangles or the ratio of the sides.

Here is one example.

Problem

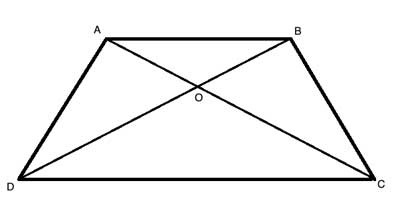
ABCD is a trapezoid (AB||CD). Its diagonals AC and BD intersect at point O. The ratio of the areas of triangles △ABO and △CDO is 16:25. Find the ratio of the area of △AOD to the area of the trapezoid.

Strategy for finding the ratio of area of triangles in a trapezoid

Problems that require find the ratio of areas or the ratio of line segments often rely on using similar triangles and using the fact that if ΔABC∼ ΔDEF, then AB/DE=BC/EF=AC/DF.

In other cases, if we are just comparing areas of triangles, they often use the fact that the ratio of areas of triangles with the same base is equal to the ratio of their heights, and the ratio of areas of triangles with the same height is equal to the ratio of their bases . An example of such a problem can be found on this page.

So in this problem - we have both! The diagonals of a trapezoid create two similar triangles (△ABO and △CDO), and several pairs of triangles with the same base (△ACD and △BDC; △DBA and △CAB) or the same height (△ABO and △ADO; △BAO and △BOC).

And one additional hint in the problem statement is that the ratio between the two triangles △ABO and △CDO is 16:25.

This is both a hint to which triangles are similar (△ABO and △CDO) and what the scale factor is - since we know that the ratio of the areas of similar triangles is the scale factor squared, and both 16 and 25 are squares of integers (4 and 5 respectively).

Proof

(1) AB||CD //Given
(2) ∠ACD≅ ∠CAB //Alternating interior angles between two parallel lines
(3) ∠ABD ≅ ∠BDC //Alternating interior angles between two parallel lines
(4) ∠BOA ≅ ∠DOC //Vertical angles
(5) ΔABO∼ ΔCDO //(2), (3), (4), Angle-Angle-Angle
(6) Area_ABO/Area_CDO=16/25 //Given
(7) AO/OC=BO/OD=√(16/25)=⅘ //The ratio of areas of similar triangles is the scale factor squared
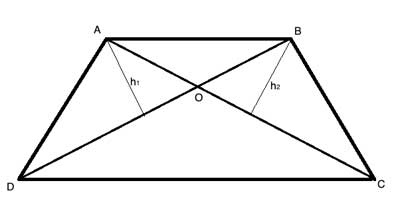
(8) Area_ABO/Area_ADO=⅘ //The ratio of areas of triangles with same height is the same s the ratio of their bases
(9) Area_ABO/Area_BOC=⅘ //The ratio of areas of triangles with same height is the same s the ratio of their bases

Set Area_ABO=16k. Then Area_CDO=25k, and Area_ADO=Area_BOC=20k.

(10) Area_ABCD=Area_ABO+Area_ADO+Area_CDO+Area_BOC=16k+20k+25k+20k=81k|
(11) Area_AOD/Area_ABCD=20k/81k=20/81