The area of a triangle is given by the formula (base · height)/2. Triangles that have the same base will have areas whose ratio is the same as the ratio of their heights:
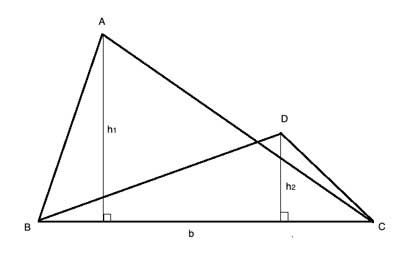
In the above drawing, triangle ΔABC and triangle ΔDBC have the same base, BC, which has length b. Their areas are thus AreaABC= (b · h1)/2 and AreaDBC= (b · h2)/2. And so the ratio of the areas is AreaABC/AreaDBC= [(b · h1)/2]/[(b · h2)/2]= h1/ h2, or simply the ratio of their heights.
And similarly, triangles with the same height will have areas whose ratio is the same as the ratio of their bases:
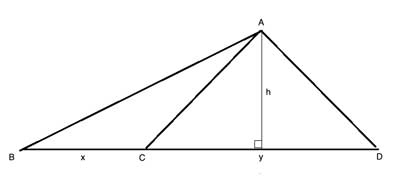
Here, triangle ΔABC and triangle ΔACD have the same height (note that the height of an obtuse triangle like ΔABC can be outside the triangle!), h. Their areas are thus AreaABC= (x · h)/2 and AreaACD= (b · y)/2. And so the ratio of the areas is AreaABC/AreaACD= [(b · x)/2]/[(b · y)/2]= x/ y, or simply the ratio of their bases.
Triangles with the same height are often found between two parallel lines - like in this problem.
Let's look at a (difficult!) geometry problem that makes use of the above property.
Problem
ABCD is a deltoid, and line AE is parallel to BC. Triangle ΔAEB (the shaded area) has an area of 30. The ratio of the lengths of segments DE and EC is 4:3, or 3|DE|=4|EC|. What is the area of the deltoid?
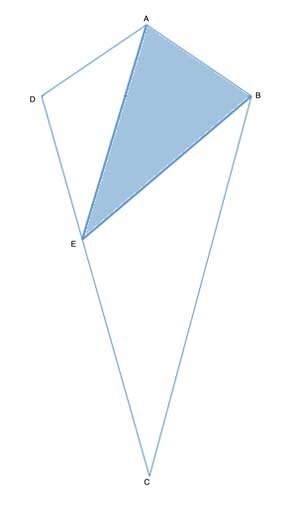
Strategy
Since we are asked to find the area of a shape, and we know the ratio of a couple of line segments, this is a hint to try and find triangles with the same height (or same base) as the one where we know the area.
The tricky thing here is to construct such triangles. We said, above, that triangles with the same height are often found between two parallel lines, and we have such parallel lines (AE||BC) - so we'll try to construct such triangles between those two lines.
Solution
Let's draw the diagonal AC. We now have two triangles with the same base - ΔBAE and ΔCAE, (AE is the base of both of them), and also the same height, since they are between two parallel lines. It is easier to see this if we extend the base, AE.
Now draw the height of ΔCAE, CF, to the extended base. GBCF is a rectangle - since AE||BC (given) and CF||BG as they are both perpendicular to GF. So CF=BG.
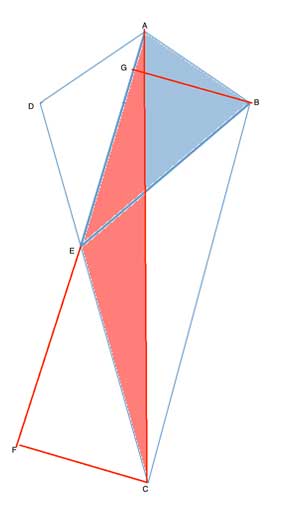
But if ΔBAE and ΔCAE have the same base and the same height, the have the same area! The area of ΔCAE is then also 30.
Now let's look at triangles ΔADE and ΔCAE. They both have the same height (they share a common vertex - A, and their bases, DE and EC, are on the same line). So the ratio of their areas is the same as the ratio of their bases - which is given (4:3).
So if the area of ΔCAE is 30, the area of ΔADE is 30*4/3=40. The combined areas of ΔADE and ΔCAE is 30+40=70, and they form a triangle (ΔADC) which is half of the deltoid, so the total area of the deltoid is 140.
