When we inscribe a kite is in a circle, all four of the kite's vertices lie on the circle's circumference.
In today's lesson, we will show that in the case of a kite inscribed in a circle, the axis of symmetry of the kite is the circle's diameter.
This is a pretty straightforward geometry proof, so today's lesson is going to be rather short.
Problem
ABCD is a kite that is inscribed in circle O. Show that AC is the diameter of the circle.
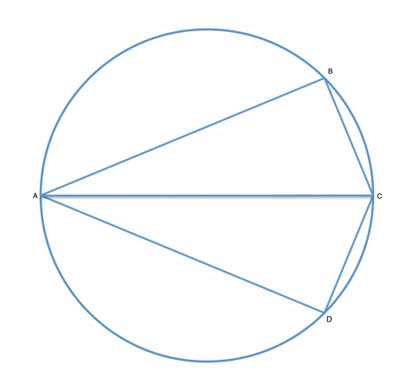
Strategy
We have previously discussed which quadrangles can be inscribed in a circle, and we have shown that such quadrangles have opposing angles that are supplementary. Meaning, they add up to 180°.
In addition, we also know that in a kite, the opposing angles on either side of the axis of symmetry are equal.
Now let's go ahead and put these two facts together. We see that this kite's opposing angles are both supplementary and equal, which means they must be 90° each. And by the inscribed angle theorem, they subtend an arc that is 180° - and thus the chord of that arc is the diameter.
Proof
Axis of symmetry of a kite inscribed in a circle:
(1) m∠ABC + m∠CDA= 180° //Opposing angles of an inscribed quadrangle are supplementary
(2) m∠ABC = m∠CDA //Opposing angles on either side of a kite's axis of symmetry are equal.
(3) m∠ABC = m∠CDA =90° //(1), (2), Transitive property of equality and algebra.
(4) Arc(ABC)=Arc(CDA) = 180° //(3), Inscribed angle theorem
(5) AC is the diameter of O //Definition of diameter