One of the proofs done by Euclid in his "Elements" book, where he laid the foundation for geometry, is that if you draw lines parallel to the sides of a parallelogram and through any point on the diagonal of a parallelogram, then the two parallelograms above and below that diagonal are equal in area. We'll repeat the proof here.
Problem
ABCD is a parallelogram, and DB is one of its diagonals. FH||AD and EG||DC. Show that the area of AEKF is equal to the area of HKGC.
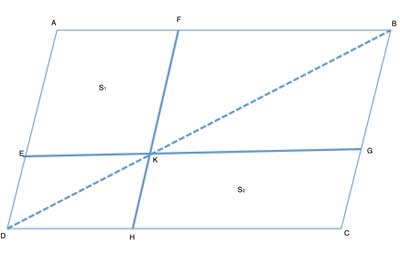
Strategy
We first note that because EG and FH were drawn parallel to two pairs of parallel sides (AB and DC, AD and BC, respectively), all four quadrilaterals AEKF, EDHK, FKGB and HKGC are themselves parallelograms.
To find the area of a parallelogram, we usually need to find the length of a side, and the height - but none of these are available here.
So we will need to use another strategy. Since we don't actually need to find the area of AEKF or HKGC, just to show that they are equal, we will try to do this using another technique we've used in the past, in this lesson or here - subtracting known areas to arrive at the unknown ones.
We have previously shown, in the process of proving that the two pairs of opposite angles of a parallelogram are congruent, that the parallelogram's diagonal bisects it into two congruent triangles, so the area of ΔABD is the same as the area of ΔBDC.
But as the smaller quadrilaterals, EDHK and FKGB themselves parallelograms that also share the same diagonal, by the above logic the area of ΔEDK is the same as the area of ΔKDH. And the area of ΔBFK is the same as the area of ΔBGK.
Subtracting the equal areas of the smaller triangles from the equal areas of the larger triangle leaves us with the areas of the two parallelograms which are equal.
Proof
(1) AD||BC //Given. ABCD is a parallelogram
(2) AB||DC //Given. ABCD is a parallelogram
(3) FH||AD // Given
(4) EG||DC // Given
(5) EDHK is a parallelogram //(3), (4), defintion of a parallelogram
(6) FKGB is a parallelogram //(3), (4), defintion of a parallelogram
(7) ΔEDK ≅ ΔKDH //(5), The diagonal of a parallelogram bisects it into two congruent triangles
(8) ΔBFK ≅ ΔBGK //(6), The diagonal of a parallelogram bisects it into two congruent triangles
(9) ΔABD ≅ ΔBDC //(The diagonal of a parallelogram bisects it into two congruent triangles
(10) Area(ABD) = Area(BDC) //areas of congruent triangles equal
(11) Area(BFK)=Area(BGK) //areas of congruent triangles equal
(12) Area(EDK)=Area(KDH) //areas of congruent triangles equal
(13) Area(ABD)-Area(BFK)-Area(EDK)=Area(BDC)-Area(BGK)-Area(KDH) //(10), (11), (12), Transitive and Subtraction properties of equality
(14) Area(S1)=Area(S2)
