Applying the Scale Factor of Similar Triangles to the Perimeter

The scale factor of two similar triangles (or any geometric shape, for that matter) is the ratio between two corresponding sides.

In today’s lesson, we will show that this same scale factor also applies to the ratio of the two triangles’ perimeter. This is fairly easy to show, so today’s lesson will be short.

Problem

Two triangles, ΔABC and ΔADE are similar, ΔABC∼ ΔADE. The scale factor, AB/AD is 6/5. Find the ratio of the perimeters of the two triangles.

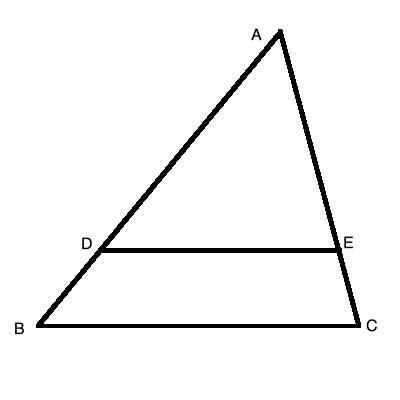
Strategy

We will use the definition of the scale factor to define one set of sides in terms of the other set of sides, Then, apply the definition of perimeter. and write out the perimeter of both triangles in using one set of sides.

Solution

(1) ΔABC∼ ΔADE //Given
(2) AB/AD = 6/5 //Given
(3) BC/DE = 6/5 //(1), (2), scale factor is the same for all sides in similar triangles.
(4) AC/AE = 6/5 //(1), (2), scale factor is the same for all sides in similar triangles.
(5) AB = 6/5*AD // rearrange (2)
(6) BC = 6/5*DE // rearrange (3)
(7) AC = 6/5*AE // rearrange (4)
(8) P_ABC=AB+BC+AC //definition of perimeter
(9) P_ADE=AD+DE+AE //definition of perimeter
(10)P_ABC=6/5*AD+6/5*DE+ 6/5*AE //(8), (5), (6) , (7), Transitive property of equality
(11)P_ABC=6/5*(AD+DE+AE) //(10), Distributive property of multiplication
(12) P_ABC=6/5*P_ADE //(11), (9), Transitive property of equality
(13) P_ABC/P_ADE=6/5

And so we have easily shown that the scale factor of similar triangles is the same for the perimeters.