A parallelogram is defined as a quadrilateral where the two opposite sides are parallel. One of the properties of parallelograms is that the opposite angles are congruent, as we will now show.
Since this a property of any parallelogram, it is also true of any special parallelogram like a rectangle, a square, or a rhombus.
Problem
ABCD is a parallelogram, AD||BC and AB||DC. Prove that ∠BAD ≅ ∠DCB and that ∠ADC ≅ ∠CBA

Strategy
There are two ways to go about this. The first is to use congruent triangles to show the corresponding angles are congruent, the other is to use the Alternate Interior Angles Theorem and apply it twice.
Let's use congruent triangles first because it requires less additional lines. Draw the diagonal BD, and we will show that ΔABD and ΔCDB are congruent.
To show these two triangles are congruent we'll use the fact that this is a parallelogram, and as a result, the two opposite sides are parallel, and the diagonal acts as a transversal line.
The diagonal is a common side, and it is also a transversal that intersects both pairs of opposite sides of the parallelogram - creating two pairs of congruent alternate interior angles.
The triangles ΔABD and ΔCDB are congruent based on the angle-side-angle postulate, and the opposite angles of the parallelogram are corresponding angles of these congruent triangles so they are congruent (using the angle addition theorem for one of the pairs).
Proof
(1) ABCD is a parallelogram //Given
(2) AD || BC //From the definition of a parallelogram
(3) ∠ADB ≅ ∠CBD //Alternate Interior Angles Theorem
(4) AB || DC //From the definition of a parallelogram
(5) ∠DBA ≅ ∠CDB //Alternate Interior Angles Theorem
(6) BD= BD // Common side, reflexive property of equality
(7) ΔABD ≅ ΔCDB // (3), (6), (5) Angle-Side-Angle postulate
(8) ∠BAD ≅ ∠DCB // Corresponding angles in congruent triangles (CPCTC)
(9) m∠ADC = m∠ADB+m∠BDC //angle addition theorem
(10) m∠CBA = m∠CBD+m∠DBA //angle addition theorem
(11) m∠ADC = m∠CBD+m∠BDC //(3), (7), substitution
(12) m∠ADC = m∠CBD+m∠DBA //(5), (9), substitution
(13) m∠CBA = m∠ADC //(10), (8), transitive property of equality
(14) ∠CBA ≅ ∠ADC //(11), definition of congruent angles
Another way to prove this
Now let's do it the other way, without triangle congruency. We'll draw the other diagonal, AC:
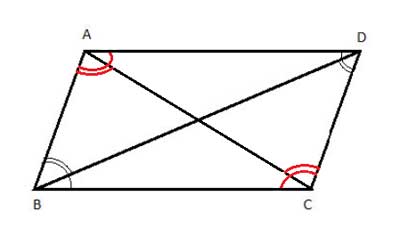
Both diagonals, AC And BD, are transversal lines the intersect both sets of parallel lines, each creating two sets of equal, alternating interior angles, and with the angle addition postulate, the sum of these partial angles is equal.
There are a lot of equations in what follows because I am proving it in a very formal way. But for simplicity's sake, what I am doing is this:
The angles marked with one arc (black ones and red ones) are equal to each other (single black arc equal to single black arc, singe red arc equal to single red arc). The angles marked with two arcs are equal to each other (double black arcs equal to double black arcs, double red arcs equal to double red arcs).
So adding up single black arc with double black arc on opposite sides of the parallelogram gives equal angles, and adding up single red arcs with double red arcs on opposite sides of the parallelogram also gives equal angles.
So, starting with diagonal BD, as above:
Proof
(1) ABCD is a parallelogram //Given
(2) AD || BC //From the definition of a parallelogram
(3) ∠ADB ≅ ∠CBD //Alternate Interior Angles Theorem
(4) AB || DC //From the definition of a parallelogram
(5) ∠DBA ≅ ∠CDB //Alternate Interior Angles Theorem
And now, with diagonal AC:
(6) ∠DAC≅ ∠BCA //Alternate Interior Angles Theorem
(7) ∠BAC≅ ∠DCA //Alternate Interior Angles Theorem
and adding partial angles up with the angle addition theorem:
(8) m∠ADC = m∠ADB+m∠BDC //angle addition theorem
(9) m∠CBA = m∠CBD+m∠DBA //angle addition theorem
(10) m∠ADC = m∠CBD+m∠BDC //(3), (8), substitution
(11) m∠ADC = m∠CBD+m∠DBA //(5), (10), substitution
(12) m∠CBA = m∠ADC //(11), (9), transitive property of equality
(13) ∠CBA ≅ ∠ADC //(11), the definition of congruent angles
And we can do the same for the other set of angles.
(14) m∠BAD = m∠BAC+m∠CAD //angle addition theorem
(15) m∠DCB = m∠DCA+m∠ACB //angle addition theorem
(16) m∠BAD = m∠DCA+m∠CAD //(7), (14), substitution
(17) m∠BAD = m∠DCA+m∠ACB //(6), (16), substitution
(18) m∠BAD = m∠DCB //(15), (17), transitive property of equality
(19) ∠BAD ≅ ∠DCB //(18), the definition of congruent angles
Thinking "Outside the Box"
Here's a third way to solve this, without any diagonals. Let's extend the sides AD and AB beyond the edges of the parallelogram, to points T and P, respectively:
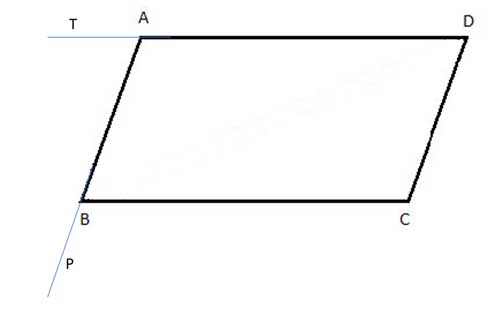
Now, since AB||CD, ∠TAB ≅ ∠ADC, as corresponding angles of parallel lines. And as AD||BC, ∠TAB ≅ ∠ABC, as alternate interior angles. So by the transitive property of equality, ∠ADC ≅ ∠ABC.
Similarly, since BC||AD, ∠PBC ≅ ∠BAD, as corresponding angles of parallel lines. And as AB||CD, ∠PBC ≅ ∠BCD, as alternate interior angles. So by the transitive property of equality, ∠BAD ≅ ∠BCD.
This is the shortest proof- but requires thinking "Outside the Box", or in this case, outside the parallelogram.
Proof #3
(1) ABCD is a parallelogram //Given
(2) AB || CD //From the definition of a parallelogram
(3) ∠TAB ≅ ∠ADC //Corresponding angles of parallel lines
(4) AD || BC //From the definition of a parallelogram
(5) ∠TAB ≅ ∠ABC //Alternate interior angles
(6) ∠ADC ≅ ∠ABC //(3) , (5) , Transitive property of equality
(7) BC || AD //From the definition of a parallelogram
(8) ∠PBC ≅ ∠BAD //Corresponding angles of parallel lines
(9) AB || CD //From the definition of a parallelogram
(10) ∠PBC ≅ ∠BCD //Alternate interior angles
(11) ∠BAD ≅ ∠BCD //(8) , (10) , Transitive property of equality
