We have shown that in any parallelogram, the opposite angles are congruent. Since a rhombus is a special kind of parallelogram, it follows that one of its properties is that both pairs of opposite angles in a rhombus are congruent.
But since in a rhombus all sides are equal, it is easier to prove this property than for the general case of a parallelogram, and this is what we will do here.
Problem
ABCD is a rhombus. Show that the opposite angles are congruent.
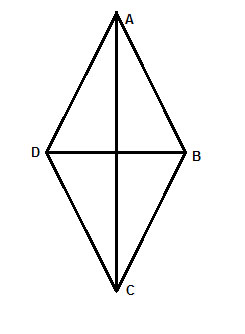
Strategy
We could do this the way we did it for the general case of a parallelogram, using the fact that both pairs of opposite sides are parallel, and so their alternating interior angles are congruent.
Then add up to the two alternating interior angles that make up the angle at the vertex using the angle addition postulate to show they are congruent.
But as the sides of the rhombus are all equal, it is simpler to show that the triangles created by each diagonal are congruent, using the Side-Side-Side postulate.
Proof: Rhombus Opposite Angles are Congruent
(1) AD=CD //Given, definition of a rhombus
(2) AB=CB //Given, definition of a rhombus
(3) DB=DB //Common side, reflexive property of equality
(4) ΔABC ≅ ΔADC // (3), (2), (1) Side-Side-Side postulate
(5) ∠ABC ≅ ∠ADC // Corresponding angles in congruent triangles (CPCTC)
…and it only took 5 line to prove what took 14 lines in the general case of a parallelogram!
Similarly, for the other pair of opposite angles:
(1) AD=AB //Given, definition of a rhombus
(2) CD=CB //Given, definition of a rhombus
(3) AC=AC //Common side, reflexive property of equality
(4) ΔDAB ≅ ΔDCB // (3), (2), (1) Side-Side-Side postulate
(5) ∠DAB ≅ ∠DCB // Corresponding angles in congruent triangles (CPCTC)
