A square is a geometric shape which is fully determined by the lengths of its side, a. If we know the length of the side of a square, we know its perimeter, its area, the length of its diagonals, etc.
In today's lesson, we will find the length of a diagonal of a square using three simple formulas, derived from the length of the square's side, or its perimeter, or its area.
Problem
ABCD is a square with side length a. Find the length of its diagonal, AC.
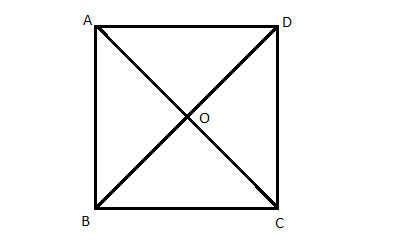
Strategy
The angles of the square are all 90°, so each one of the triangles formed by the diagonals with the sides (ΔBAD , ΔABD, ΔDCA, ΔBDC) is a right triangle.
Both legs of each one of the triangles are sides of the square so their side is known and equal to 'a'. So, pick one of these triangles, and use the Pythagorean theorem to find the length of the diagonal from the length of the side.
Proof
(1) ABCD is a square //Given
(2) ∠BAD = 90° //definition of a square
(3) BA=AD='a' //given, defintion of a square
(4) AC2=a2+a2 //(2),(3) ,Pythagorean theorem
(5) AC=√(2a2)
(6) AC=a ·√2
Having done that, let's derive similar formulas using the square's perimeter and area.
The perimeter of a square, P, is 4 times the length of the side: P=4a. So the side is P/4, and we can plug that into the formula above: AC=P/4 ·√2
And similarly, the area of a square, A, is the side squared, or a2. A=a2. So the side is √A and we can plug that into the formula above: AC=√A ·√2=√(2A)
