In today's lesson, we will find a formula for the length of a line parallel to the bases of a trapezoid that splits it into two similar trapezoids.
We have looked at a couple of special lines within a trapezoid that are parallel to the bases - the area bisector which partitions the trapezoid into two smaller trapezoids with equal areas, and the midsegment, which connects the midpoints of the two legs.
And we've derived a formula for the length of those lines using the length of the bases of the original trapezoid.
Now let's look at another such line parallel to the bases - one that partitions the trapezoid into two similar trapezoids. And as we did before, we'll derive a formula for its length using the length of the bases of the original trapezoid.
Problem
ABCD is a trapezoid, AB||CD. EF is a line parallel to the bases (EF||AB||CD) which creates two similar trapezoids: ABFE ∼ EFCD. Find a formula for the length of FE in terms of the lengths of AB and CD.
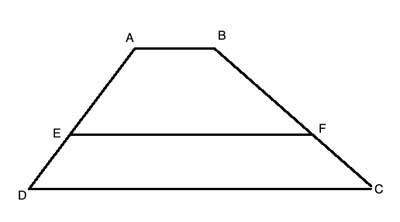
Solution
In geometry, shapes are said to be similar if the ratio between their corresponding sides is equal.
So if the two trapezoids created by this parallel line are similar, the ratio between the top base of the top trapezoid and the top base of the bottom trapezoid will be equal to the ratio between the bottom base of the top trapezoid and the bottom base of the bottom trapezoid.
Let's call the top base ‘a’ (AB=a), the bottom base ‘b’ (CD=b), and the middle line ‘c’ (EF=c).
Then a/c = c/b, and rearranging, c2=ab, and c=√(ab)
So c is the geometric mean (average) of a and b.