There are a number of interesting features of lines drawn parallel to the bases of a trapezoid. We saw one of these in this problem- a line parallel to the bases and connecting the midpoints of the legs.
If the bases of the trapezoid are a and b, that line's length is equal to ½(a+b). We will later deal with another such interesting line - a line parallel to the bases of the trapezoid which partitions it into two similar trapezoids.
But here, we'll consider the following line- drawn parallel to the bases of the trapezoid, and partitioning the trapezoid into 2 equal areas. This line is sometimes called the area bisector.
Problem
ABCD is a trapezoid, AB||CD. Ef is parallel to the bases (EF||AB, EF||AB), and divides ABCD into two equal areas. Find a formula for the length of EF using AB and CD.
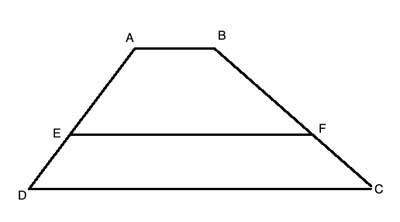
Strategy
Let's call the top base 'a', the bottom base 'b', and the middle line 'c'.
Line c creates two trapezoids within the original trapezoid. The areas of the two small trapezoids are equal, so let's call that area 'S', and the area of the big trapezoid is 2S.
We'll write out the formulas for the areas of the two small trapezoids using the bases, a, b, and c, and then use some basic algebra to solve for c, making use if the fact that the areas are equal, and that the combined heights of the smaller trapezoids is equal to the height of the large one: h1+h2=h
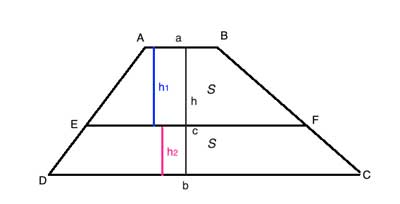
Solution
For the top small trapezoid:
(1) S=(a+c) · h1 / 2 → h1 = 2S/(a+c)
For the bottom small trapezoid:
(2) S=(b+c) · h2 / 2 → h2 = 2S/(b+c)
For the large trapezoid, h= h1+h2 and the area is 2S, so
(3) 2S = (a+b)· h /2 = (a+b)·[2S/(a+c)+2S/(b+c)]/2
(4) 1 = (a+b)/[1/(a+c) +1/(b+c)]/2 //divide both sides by 2S
(5) 2 = (a+b)/(a+c) +(a+b)/(b+c) //rearrange
(6) 2·(a+c)·(b+c) = (a+b)(b+c)+(a+b)(a+c) //common denominator and cross multiply
(7) 2ab+2ac+2cb+2c2=ab+ac+b2+bc+a2+ac+ba+bc
(8) 2c2=b2+a2
(9) c=√[(b2+a2)/2]
So c is the quadratic mean (or Root Mean Square - RMS) of the two bases of the trapezoid.
