In today's lesson, we will find the area of an irregular shape by partitioning it into triangles.
We've derived the basic formulas for the areas of regular shapes like triangles, rectangles, parallelograms and circles. But how do we proceed when presented with an irregular shape? We'll explore two approaches in today's lesson.
Problem
Find the area of the shaded shape in the following drawing:

Strategy
The Standard Approach
The typical strategy for problems of this type is to partition the irregular shape into simpler shapes. Then we use known formulas for the simple shapes to find the area of the irregular one. This strategy often works for both shapes with straight edges, as in this problem, as well as for those with curves, like finding the area of a heart shape.
In this case, a partition already suggests itself. The dashed line is the middle of the rectangle. There are three triangles, two above the dashed line and one below it. We will compute the height and base for each one.
Finding the base and height of the bottom triangle is easy. Its height is given as 2. The base can be computed to be 5.5, using the fact that the dashed line in the unshaded left-most right triangle is a midsegment - it is parallel to the base, and intersects the mid-point of the left-most side of the rectangle. So it is equal to half the base, which is given as 1. And so the area of the bottom triangle is (h x b) /2 or (2x5.5)/2 = 5.5
But now we run into a problem: What about the top two triangles? There is no way to compute the bases of the top two triangles using the information in the problem, because we have no information about point 'A' - it could be anywhere along the dashed line, changing the length of the bases without violating any of the information given.
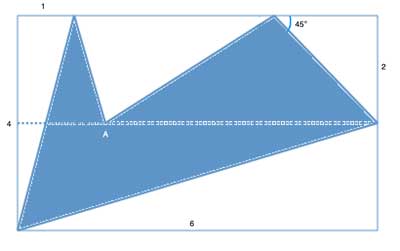
But here's an interesting trick: the height of both of these triangles is the same (2), and as we move point 'A' along the dashed line, whatever length we add to the base of one of the triangles, we subtract from the other - so the sum of the areas of the triangles remains the same, no matter where point A is!
Mathematically, if we call the length of the base of one of these triangles 'x', the other must be (5.5-x). The combined areas of these triangles is (2 ·x)/2+[2 ·(5.5-x)]/2= x+5.5-x = 5.5.
Adding the areas of the top two triangles (5.5) to the area of the bottom triangle (also 5.5) gives the area of the shaded shape - 11.
Another way to solve this problem
That previous trick is not obvious, so here's another strategy to solve this problem and find the area of an irregular shape. We'll find the area of the shaded part by first finding the area of the non-shaded parts, and then subtract those from the area of the rectangle- and what remains is the shaded area!
The area of the rectangle is simple, it is length x height, or 6x4=24.
The non-shaded area is composed of 4 triangles.
The leftmost one is a right triangle with a base of 1 (given) and a height of 4 (given), so its area is 1x4/2= 2.
The bottom one is a right triangle with a base of 6 (given) and a height of 2 (given), so its area is 6x2/2= 6.
The right one is a right triangle with a base of 2 (given). Since it is a right triangle with one angle equal to 45°, it is a 45-45-90 triangle. So the height must be 2 as well. Its area is then 2x2/2= 2.
Finally, the top triangle has a height of 2 (given). Its base is the length of the rectangle (6), minus the base of the other two triangles - 1 and 2, respectively. So it has a base of length 3, and an area of 3x2/2=3.
The sum of all these unshaded triangles is 2+6+2+3=13, and if we subtract it from the area of the rectangle (24) we have the shaded area as 24-13=11.
