The triangle midsegment theorem states that the midsegment is parallel to the third side, and its length is equal to half the length of the third side, and its converse states that if a line connecting two sides of a triangle is parallel to the third side and equal to half that side, it is a midsegment.
There is an additional converse theorem to the midsegment theorem - if a line connecting two sides of a triangle is parallel to the third side and intersects one side's midpoint, it is a midsegment - it bisects the other side and is equal to half the third side.
Problem
In triangle ΔABC, DE is parallel to BC, and BD=DA . Show that DE is a midsegment. In other words: Show that CE=EA and that its length is equal to half the length of BC.
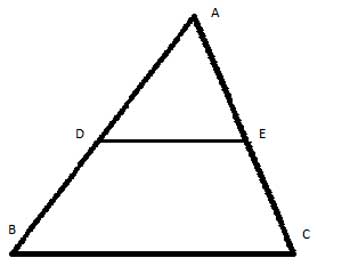
Strategy
Recall that when we proved the converse midsegment theorem, we did so by extending DE, constructing a quadrilateral and proving it is a parallelogram.
So let's try the same approach here: We'll draw a line through point C that is a parallel to AB, and extend DE so that it intersects that line at point F. (We know we can do this because of the parallel line axiom (”for every line and every point not on that line, there is one straight line that passes through that point, and never intersects the first line“).

Now, DE is parallel to BC, as given in the problem statement, and CF is parallel to BD, because we constructed it that way. So BDFC is a parallelogram (by the definition of a parallelogram - A quadrangle in which both pairs of opposite sides are parallel to each other.)
And we can now proceed in the same manner as we did when we proved the first converse midsegment theorem - we will show that the triangles ΔADE and ΔCFE are congruent, and from this show that CE=EA. Now, since BD=DA and CE=EA, DE is a midsegment, and by the midsegment theorem, is equal to half of BC.
Proof
(1) CF||BD //Construction
(2) DE||BC //Given
(3) DFCB is a parallelogram //(1), (2),definition of a parallelogram
(4) BD=CF //(3), Opposite sides of parallelogram
(5) BD||CF //(3), Opposite sides of parallelogram
(6) ∠DAE ≅ ∠FCE // Alternate Interior Angles Theorem
(7) ∠AED ≅ ∠CEF // Vertical angles
(8) BD=DA // Given
(9) DA=CF //(4), (8), transitive property of equality
(10) ΔADE ≅ ΔCFE // Angle-Angle-Side
(11) CE=EA // corresponding sides in congruent triangles, (CPCTC)
(12) DE is a midsegment //((8), (11), definition of a midsegment
(13) DE=½BC //Midsegment theorem
