Equilateral Triangle: Find its Area from the Radius of an Inscribed Circle

This problem is the opposite of the one where we found the area of the inscribed circle using the length of the side of the equilateral triangle. Here, we will use the circle's radius to find the area of the triangle.

Problem

Circle O with radius r is inscribed in an equilateral triangle. Find the area of the triangle in terms of r.

Strategy

The area of the triangle is comprised of the area of 6 triangles created by drawing the radii to the tangent points, and connecting the triangle's vertices to the circle's center. Let's draw two of those triangles:

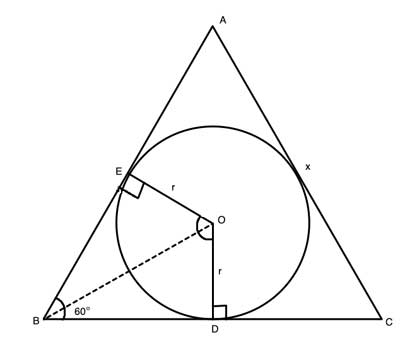
The two radii, OD and OE, are equal to each other. From the Two Tangent theorem, we know that BD=BE, so ΔBOD is congruent to ΔBOE by the Side-Side-Side postulate. That means that ∠OBE≅∠OBD, and since m∠ABC=60° as an angle of an equilateral triangle, m∠OBD=30°.

The radii are perpendicular to the sides of the triangle (AB and BC) at the point where they meet the tangent, so ΔBOD is a 30-60-90 triangle. So BD=r·√3, as the long leg of a 30-60-90 right triangle where the short leg is r.

The area of each one of the small triangles is given by A_small=base·height/2, or A_small=r·r·√3/2=r²·√3/2. We have six of these triangles in the equilateral triangle, so its area is A_equilateral= 6·A_small=6·r²√3/2=3r²√3.

Solution

(1) OE = OD = r //radii of a circle are all equal to each other
(2) BE=BD // Two Tangent theorem
(3) OB=OB //Common side, reflexive property of equality
(4) ΔBOD ≅ ΔBOE //Side-Side-Side postulate
(5) ∠OBE≅∠OBD //corresponding angles in congruent triangles
(6) m∠ABD = 60° //Given, ΔABC is equilateral
(7) m∠OBD = 30° // (5) , (6)
(8) m∠ODB=∠OEB=90° //radii are perpendicular to tangent line
(9) ΔBOD is a 30-60-90 triangle //(7), (8)
(10) BD= r·√3 //Properties of 30-60-90 triangle
(11) A_ΔBOD=base·height/2=r·r·√3/2=r²·√3/2
(12) A_ΔABC=6·A_ΔBOD=6·r²√3/2=3r²√3