A kite is a quadrilateral with two pairs of sides that are equal. A kite has four internal angles, two of these are the opposite angles between the unequal edges, and two are the opposite angles between the equal edges. It is fairly easy to show that the angles between the unequal edges of a kite are congruent. We will prove this by using congruent triangles.
On the other hand, the pair of opposite angles between the edges that are equal can be of any size, and have no special relationship to each other.
Problem
ABCD is a kite. Show that ∠ABC≅∠ADC
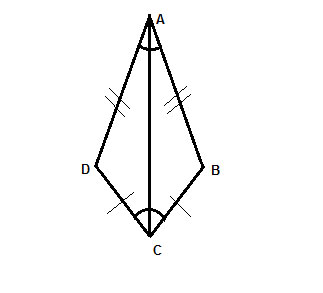
Strategy
In general, a common tool for showing that two angles are congruent is to show that they are corresponding parts of congruent triangles. We will show that the two angles between the unequal sides of the kite are congruent using this method. To do this, we'll create two triangles in which they are corresponding angles, by drawing the diagonal AC.
Proof: Angles Between the Unequal Edges of a Kite are Congruent
(1) ABCD is a kite //Given
(2) AB=AD //definition of a kite
(3) BC=CD //definition of a kite
(4) AC=AC //Common side, reflexive property of equality
(5) △ABC≅△ADC //Side-Side-Side postulate.
(6) ∠ABC≅∠ADC //Corresponding angles in congruent triangles (CPCTC)
The diagonal AC is known as the axis of symmetry of the kite. This means that if we "fold" the kite of this axis, or if we hold up a mirror on the line, the two halves will match. This is also known as "Reflection Symmetry".
We know that the two sides will match in length, because that is the defintion of a kite - a quadrilateral with two pairs of adjacent sides of equal length. And we have now shown that because the angles between the unequal edges of a kite are congruent, they will match as well.