Three points in a plane that are not all on the same line (not collinear) define a triangle, and any triangle can be circumscribed by a circle. So, three points in a plane also define a circle. In today's problem, we will find the area of a circle using just 3 points.
Some version of this problem often appears in the SAT Math 2 subject test!
Problem
Three points of a circle on the x-y coordinate plane have coordinates (-5,-6); (-5, -2) and (1, -2) respectively. Find the area of the circle.
Strategy
To find the area of a circle, we need its radius or diameter - but neither one is given in the problem, so we will probably need to figure out the radius from the given coordinates. Let's draw the circle and points on the x-y plane:
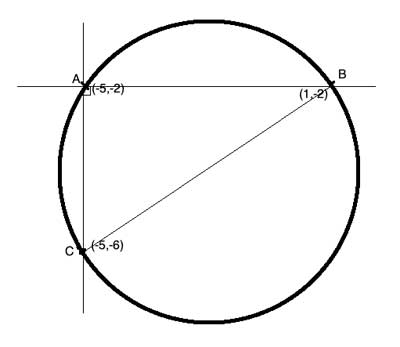
We see that two of the points, A & B, have the same y coordinate (-2), so they both lie on the same horizontal line (y=-2) that is parallel to the x axis.
The other two points, A & C, have the same x coordinate (-5), so they both lie on the same horizontal line (x=-5) that is parallel to the y axis.
This means that the lines AB and AC are perpendicular to each other and that ∠CAB is a right angle, so m∠CAB= 90°. But ∠CAB is also an inscribed angle in the circle, so it is equal to half the central angle of the arc it subtends - so that arc (BC) must be 180°, which means that line CB is the diameter!
We can find the length of CB using the Pythagorean theorem, divide by two to get the radius, and we the area of the circle is π*r2.
Solution
(1) AB⊥AC //given, using the coordinates of points A, B and C
(2) m∠CAB= 90° //Definition of perpendicular lines
(3) Arc CB= 180° //Inscribed angle theorem
(4) r=CB/2 //CB is the diameter
(5) CB2=AB2+AC2 //Pythagorean theorem
(6) CB2=36+16=52
(7) CB=√52
(8) r=(√52)/2 //(4)
(9) Areacircle=π*r2=π*52/4=13π
