In geometry, "circumscribed" means "to draw around." A circumscribed circle is a circle that is drawn around a polygon so that it passes through all the vertices of a polygon inscribed in it.
All triangles have circumscribed circles, and in this lesson, we will devise a method to find that circle.
Problem
In triangle △ABC, D and E are the midpoints of sides AB and AC, respectively. DO and EO are perpendicular to AB and AC. Show that AO=BO=CO.
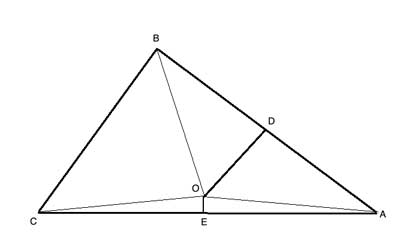
Strategy
The simplest way to show line segments in a triangle are equal is with triangle congruency. Here, we have two pairs of triangles: (△AOE, △COE) and (△AOD, △BOD).
For each pair, we are given one equal side - since points E and D are the midpoints of their respective sides, and one equal angle - since DO and EO are perpendicular to each side, forming a linear pair of two right angles.
This makes it easy to show, that for each pair, the triangles are congruent, and by the transitive property of equality, AO=BO=CO.
Proof
(1) CE=EA //given, E is the midpoint of AC
(2) OE=OE //Reflexive property of equality, common side
(3) OE⊥AC //given
(4) m∠OEC=m∠OEA=90° //(3) , Linear pair formed by perpendicular lines
(5) △AOE≅ △COE //Side-Angle-Side postulate
(6) AO=CO //Corresponding sides of congruent triangles (CPCTC)
(7) BD=DA //given, D is the midpoint of AB
(8) OD=OD //Reflexive property of equality, common side
(9) OD⊥AB //given
(10) m∠ODB=m∠ODA=90° //(9), Linear pair formed by perpendicular lines
(11) △AOD≅ △BOD //Side-Angle-Side postulate
(12) AO=BO //Corresponding sides of congruent triangles (CPCTC)
(13) AO=BO=CO //(6),(12), Transitive property of equality
The point O is thus equidistant from all three of the triangle's vertices, so if we draw a circle by taking a compass, centering it on O and using OA as the radius, it will pass through A, B and C and we will have a circumscribed circle for triangle △ABC.
