Using the Tangent-Chord Theorem, it is simple to prove the third theorem which provides a relationship between lines in circles – the Tangent-Secant Theorem (the other two being the Intersecting Secants Theorem and the Intersecting Chords Theorem).
Problem
AB is tangent to circle O, and AC is a secant line intersecting the circle at points C and D. Prove that AB2=AC · AD
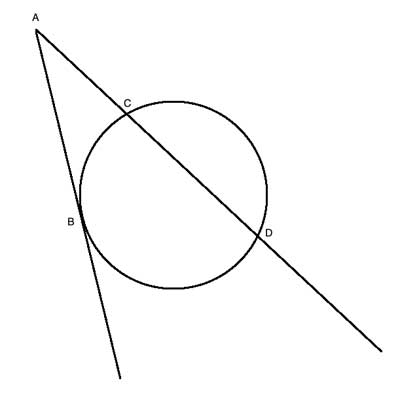
Strategy for proving the Tangent-Secant Theorem
Just as we did in the other two theorems which provide a relationship between the lengths of line segments of tangents or chords, we are pointed in the direction of using triangle similarity by the fact that we need to prove a relationship involving the product of lengths of lines ( AB2=AC · AD).
So let’s construct triangles in which AB, AC and AD are sides, and show they are similar:
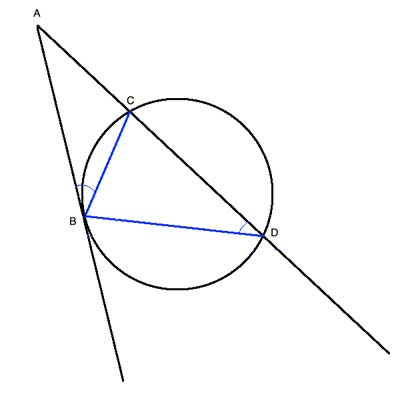
Looking at triangles ΔABC and ΔADB, we see they share one angle, ∠BAC. Using the Tangent-Chord Theorem, we see that ∠ABC ≅ ∠ADB, so the two triangles are similar, and it follows that AB2=AC · AD.
Proof
(1) ∠BAC ≅ ∠BAC //Common angle
(2) ∠ABC ≅ ∠ADB //Tangent-Chord Theorem
(3) ∠ACB ≅ ∠ABD //Sum of Angles in a Triangle
(4) ΔABC∼ ΔADB //Angle-Angle-Angle
(5) AB2=AC · AD //(5), property of similar triangles
