In today's lesson, we will present a detailed, step-by-step proof of the Intersecting Secants Theorem, using properties of similar triangles. This is a fairly simple proof, so today's lesson will be short.
A secant is a line that extends from a point outside the circle and goes through the circle. It intersects the circle at two points, and the line segment between those two points inside the circle is a chord.
Similar to the Intersecting Chords Theorem, the Intersecting Secants Theorem gives the relationship between the line segments formed by two intersecting secants.
Problem
AB and AC are two secant lines that intersect a circle. Show that AD⋅AB=AE⋅AC.
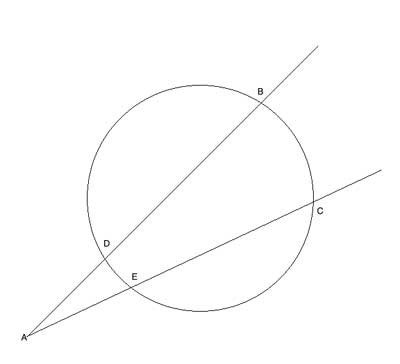
Strategy
We are asked to show the relationship between line segment lengths as a product of their lengths. This is a clear hint to use triangle similarity, since we know that in similar triangles ΔABC∼ ΔDEF, AB*EF = BC*DE.
So let's draw a couple of triangles in which the sides AD, AB, AE and AC are sides:
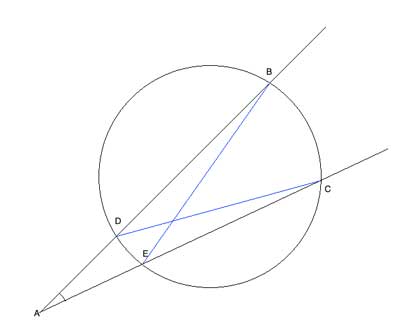
We can now easily show the two triangles ΔABE and ΔACD are similar (one shared angle, one pair of congruent angles which subtend the same arc), and the required relationship immediately follows.
Proof
(1) ∠BAC ≅ ∠CAB //Common angle to both triangles, reflexive property of equality
(2) ∠ABE ≅ ∠ACD // Inscribed angles which subtend the same arc are equal
(3) ∠BEA ≅ ∠CDA //(1), (2), Sum of angles in a triangle
(4) ΔABE ∼ ΔACD //angle-angle-angle
(5) AD⋅AB = AE⋅AC //(4), property of similar triangles