The Tangent-Chord Theorem states that the angle formed between a chord and a tangent line to a circle is equal to the inscribed angle on the other side of the chord: ∠BAD ≅ ∠BCA.
Problem
Prove the Tangent-Chord Theorem.
Strategy
As we’re dealing with a tangent line, we’ll use the fact that the tangent is perpendicular to the radius at the point it touches the circle. Let’s draw that radius, AO, so m∠DAO is 90°. Let’s call ∠BAD “α”, and then m∠BAO will be 90-α. We’ll draw another radius, from O to B:
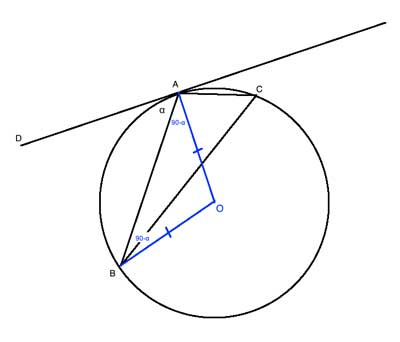
And since all radii are equal, OA=OB and we have an isosceles triangle △AOB. From the base angle theorem, m∠ABO is also 90-α. From the sum of angles in a triangle, m∠BOA=180-2·(90-α) = 2α.
Now, ∠BCA is an inscribed angle that subtends the same arc as the central angle ∠BOA, so by the inscribed angle theorem, it is equal to half of m∠BOA, or α, and ∠BAD ≅ ∠BCA.
Proof
(1) m∠DAO = 90° //Given, AD is tangent to circle O, the tangent is perpendicular to the radius
(2) m∠BAD = α
(3) m∠BAO = 90-α //(1), Angle addition postulate
(4) OA=OB //All radii of a circle are equal
(5) m∠ABO = m∠BAO //(4), base angle theorem
(6) m∠BOA=180-2·(90-α) = 2α //(5), Sum of angles in a triangle
(7) m∠BCA=½m∠BOA //Inscribed angle theorem
(8) m∠BCA=α //(6),(7)
(9) m∠BCA=m∠BAD //(2), (8), transitive property of equality
(10) ∠BAD ≅ ∠BCA //definition of congruent angles
The Tangent-Chord theorem is sometimes stated as “The angle formed by a tangent to a circle and a chord is equal to half the angle measure of the intercepted arc.” This is equivalent to what we have shown, since the angle measure of an intercepted arc is twice the angle measure of the inscribed angle that subtends it.
Now that we have shown this, it is easy to prove another relationship between tangent lines and chords – the Tangent-Secant Theorem.
