Congruent circles have the same radius length. In today's lesson, we will find the distance between the centers of two overlapping congruent circles, given the length of the overlapping arc, using properties of a rhombus.
Problem
Two congruent circles with radius 1 unit overlap, with the overlapping arc, AB, measuring π/3 units. Find the distance between the centers of the circles, OQ.
Strategy
Since the circles are congruent, they have the same radius, which is given. Let's draw them:
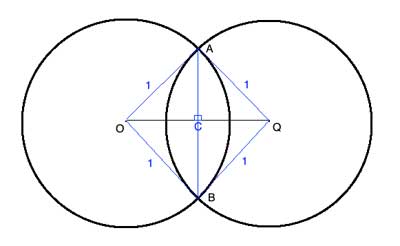
Since the radii are all equal, AOBQ is a rhombus.
In a rhombus, the diagonals are perpendicular, and bisect the angles.
So we have ∠AOC≅ ∠BOC, and triangle ΔAOC is a right triangle whose hypotenuse, OA, we know (it is the radius, given as 1).
What else haven't we used? We were given the length of the arc, AB, and haven't used that yet.
We know that an arc's length is the same proportion of the circle's circumference as the arc’s measure in degrees is of 360°. So if AB measures π/3 units, and the circle's circumference is 2*r*π , and in this case r=1, then (π/3)/2π = m∠AOB/360°, giving m∠AOB=60°.
And since the diagonals of a rhombus bisect the angles, m∠AOC=30° and triangle ΔAOC is a special 30-60-90 triangle, whose sides can all be calculated from knowing the hypotenuse.
OC is the long leg of the 30-60-90 triangle (opposite the 60° angle), so it is equal to √3/2, and since the diagonals bisect each other, OQ=2OC=√3.
Proof
(1) AO=OB=BQ=QA=1 //Given, circles are congruent with radius 1, all radii are equal
(2) AOBQ is a rhombus //(1), defintion of a rhombus
(3) ∠AOC≅ ∠BOC //(2) ,diagonals of a rhombus bisect the angles
(4) m∠OCA=90° //(2), diagonals of a rhombus are perpendicular
(5) AB = π/3 //Given
(6) (π/3)/2π = m∠AOB/360° //an arc's length has the same proportion of the circumference as the arc's angle measure has, of 360°
(7) m∠AOB= 60° //(6), solve for m∠AOB
(8) ΔAOC is a 30-60-90 triangle //(4),(7), sum of angles in a triangle
(9) OC=√3/2 //(8), OC is the long leg of a 30-60-90 triangle
(10) OQ=2OC //(2), diagonals of a rhombus bisect each other
(11) OQ=√3
