We have shown that in a rhombus the diagonals bisect the angles, using triangle congruency. We can follow the same procedure to prove that the diagonals of a rhombus are perpendicular to each other
Problem
In a rhombus ABCD, prove that the diagonals are perpendicular to each other. i.e prove that AC⊥DB.
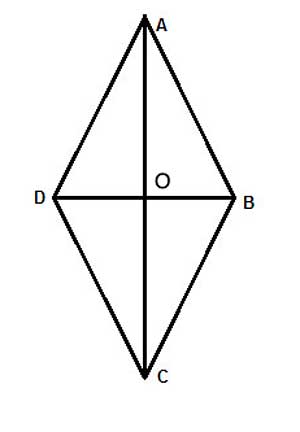
Strategy
To prove that two lines are perpendicular, when all we have are those two lines, we can use the Linear Pair Perpendicular Theorem - If two straight lines intersect at a point and form a linear pair of equal angles, they are perpendicular.
Our diagonals intersect at point O, so we'd need to show the two linear angles formed at that intersection point are equal, and we can do that with triangle congruency.
A rhombus is a parallelogram, so we will use what we already know about parallelograms - that the diagonals bisect each other.
It is then easy to show that the triangles ΔAOD and ΔAOB are congruent using the Side-Side-Side postulate, and from that that ∠AOD ≅ ∠AOB.
And now, since ∠AOD and ∠AOB are a linear pair, we use the Linear Pair Perpendicular Theorem - If two straight lines intersect at a point and form a linear pair of equal angles, they are perpendicular.
Proof
(1) ABCD is a rhombus //Given
(2) AB=AD //definition of rhombus
(3) AO=AO //Common side, reflexive property of equality
(4) BO=OD // A rhombus is a parallelogram, a parallelogram's diagonals bisect each other
(5) △AOD≅△AOB //Side-Side-Side postulate.
(6) ∠AOD ≅ ∠AOB //Corresponding angles in congruent triangles (CPCTC)
(7) AC⊥DB //Linear Pair Perpendicular Theorem
The converse of this is also true: if a parallelogram's diagonals are perpendicular, it is a rhombus.
