Radius of a Circle with an Inscribed Triangle

In today's lesson, we will learn how to find the radius of a circle with an inscribed triangle.

Many geometry problems involve a triangle inscribed in a circle, where the key to solving the problem is relying on the fact that each one of the inscribed triangle's angles is an inscribed angle in the circle.

Problem

Triangle ΔABC is inscribed in a circle O, and side AB passes through the circle's center. Find the circle's radius.

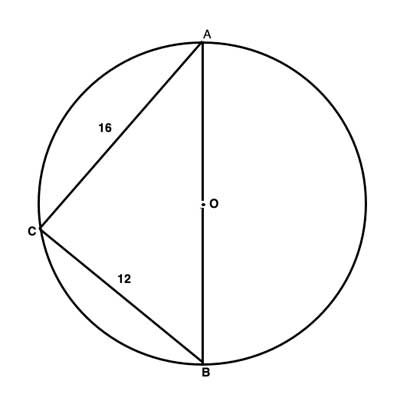
Strategy

When we need to find the length of line segments which are sides in triangles, we have a couple of handy tools. If we have a right triangle, we can use the Pythagorean Theorem, and if we have two similar triangles we can use the product property of similar triangles.

Here we have only one triangle, so let's try to see if it is a right triangle, enabling us to use the Pythagorean Theorem.

This is a problem involving a triangle inscribed in a circle. So we will see if we can make use of inscribed angles. We see that ∠ACB is an inscribed angle that subtends the diameter of the circle (the hint in the problem being that "side AB passes through the circle's center."). The diameter is half a circle, so its measure is 180°. And an inscribed angle that subtends the diameter thus measures half of 180°, or 90°.

So yes, m∠ACB=90°, and ΔABC is a right triangle.

Another useful hint that ΔABC is a right triangle is the two given sides, 12 and 16, which make up 2 of the 3 numbers that form a "Pythagorean Triple": 12, 16, 20. Pythagorean triples are 3 numbers that preserve the relationship c^{2 =} a²+b², meaning they can form the sides of a right triangle. It is useful to familiarize yourself with and memorize some of the more common Pythagorean triples, such as those listed here.

We'll use the Pythagorean Theorem to find the length of side AB, which is the hypotenuse. And since AB is the diameter, the circle's radius is half of AB.

Solution

(1) Arc_BOA = 180°  //AB is the diameter of a circle, so its arc measures half of a full circle
(2) m∠ACB=90° //Inscribed angle subtending the diameter
(3) AC²+CB²=AB² //Pythagorean Theorem
(4) AC=16 //Given
(5) CB=12 //Given
(6) 16*16+12*12=AB²
(7) 400 = AB²
(8) AB = 20
(9) r = AB/2 = 10