There are several theorems related to chords and radii or diameters that connect to them. In today's lesson, we will first prove that a diameter that bisects a chord is perpendicular to that chord and that it also bisects the arc that the chord subtends.
Problem
In circle O, the diameter AB bisects a chord, CD. Prove that AB⊥CD and that the two arcs, CB and BD are equal.
Strategy
In order to prove that two lines are perpendicular, we can use the Linear Pair Perpendicular Theorem. This theorem states that if two straight lines intersect at a point and form a linear pair of equal angles, they are perpendicular.
AB and CD intersect at point E, so we'd need to prove the angles created at that intersection point, ∠OEC and ∠OED, are equal. That is easy to do with triangle congruency, if we connect the chord's endpoints with the center, as the sides are all equal.
This will also demonstrate that the two central angles that subtend the two parts of the arc CBD are equal, proving the second part.
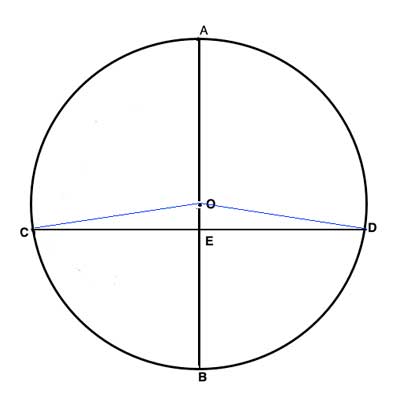
Proof
(1) CE=ED //Given, AB bisects the chord CD
(2) OE=OE // Common side, reflexive property of equality
(3) OC=OD=r // Radii of a circle are all equal
(4) ΔOEC≅ ΔOED // Side-Side-Side postulate
(5) ∠OEC ≅ ∠OED // (4), Corresponding angles in congruent triangles
(6) AB⊥CD // Linear Pair Perpendicular Theorem
(7) ∠COB ≅ ∠DOB // (4), Corresponding angles in congruent triangles
(8) ArcCB≅ArcBD //(7)
Related Proofs
Now that we have our proof, we can use the same procedure to prove the converse, that a diameter that is perpendicular to a chord bisects that chord.
And we can also now easily show that if a diameter bisects two chords, they are parallel to each other.
