A Diameter Perpendicular to a Chord

We've shown that a diameter that bisects a chord is perpendicular to that chord. Here, we will prove the converse theorem.

Problem

In circle O, the diameter AB is perpendicular to a chord CD. Prove that it bisects the chord.

Strategy

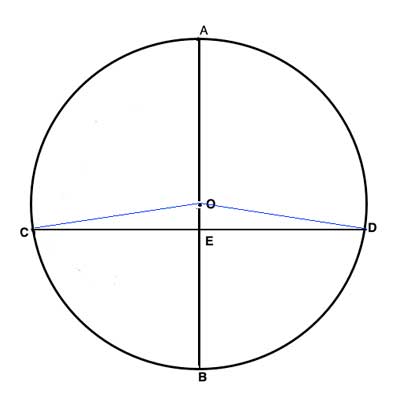
We will show that the two line segments, CE and ED, are equal, using triangle congruency. To do that we will construct triangles in which these two line segments are sides.

We can connect the chord's endpoints with the center. The connecting lines are radii of the circle, and thus equal to each other., since all the radii of a circle are equal. We will also use the fact that AB⊥CD (given in the problem statement) to prove congruency of these 2 right triangles using the Hypotenuse -Leg postulate.

Proof

(1) OE=OE // Common side, reflexive property of equality
(2) OC=OD=r // Radii of a circle are all equal
(3) AB⊥CD // Given
(4) ΔOEC≅ ΔOED // Hypotenuse-Leg
(5) CE=ED // (4), Corresponding sides in congruent triangles

And as a side benefit, we have also proven that the perpendicular diameter bisects the arc subtended by the chord, since:
(6) ∠COB ≅ ∠DOB // (4), Corresponding angles in congruent triangles
(7) Arc_CB≅Arc_BD //(6)