In today's lesson, we will show a simple formula for finding the length of an arc in a circle.
An arc is a part of the circle's circumference. A circle measures 360°, so the length of an arc that is the entire circle (an arc measuring 360°) is simply the circle's circumference, given by C=2*π*r.
A partial arc will have a length that is the same proportion of the circumference as the arc's measure in degrees is of 360°. The length of an arc measuring 90° will be a quarter of the circumference, the length of an arc measuring 45° will be an eighth of the circumference, and so on.
In general, for an arc measuring θ°, the arc length s, is s= 2*π*r*θ/360.
Problem
A CD has an area of 17.35 square inches. Find the length of a 60° arc.
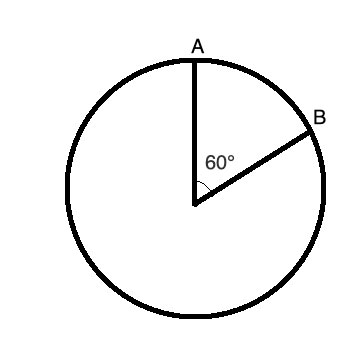
Strategy
A circle is entirely defined by its radius - so we can get the radius of the CD from its area. Once we have the radius, we will use the above formula (s= 2*π*r*θ/360) to find the arc length.
Solution: arc length formula
ACD=17.35
Acircle= π*r2
r2=17.35/π=5.5225
r=√5.5225=2.35
s= 2*π*r*θ/360= 2*π*2.35*60/360=2.46 inches