Circles: Finding the Area of a Ring

A ring is a geometric shape made up of two circles with the same center point. We call such circles "concentric". Another name for a ring is an Annulus.

Problem

A circular hot tub with radius 6 feet has a sitting area around its perimeter, with a width of 1 foot. Find the area of the sitting area.

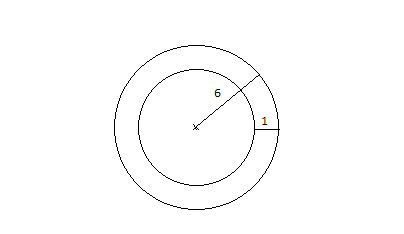
Strategy

A circle is completely defined by its radius, and its area is given by  A _circle =π*r². The tub and the sitting area form two concentric circles.

We know the radius of the outer circle (the tub) - so we can find its area. We know the width of the sitting area, from which we can calculate the inner radius (from the center of the tub to the inner edge of the sitting area), and find the area of the inner circle.

If we subtract the inner area from the outer area, we get the area of the ring, which is the sitting area.

Solution

(1) R_tub= 6
(2) A_outer =π*R²=π*6²=36π
(3) r_inner= 6-1=5
(4) A_inner =π*r²=π*5²=25π
(5) A_ring =A_outer-A_inner=36π-25π=11π≈34.56

From that last line in the solution, we can see that more generally, the area of the ring is the difference between the areas of the two circles, or A_ring =A_outer-A_inner. But we can express the difference between these two areas in a compact form as A_outer-A_inner=π(R²_outer-r²_inner)