In many of the problems involving similar triangles, you will be asked to prove that the triangles are similar.
The easiest way to do this is to show that all the angles are congruent or have an equal measure.
We can use one of the tools are our disposal to show angles are congruent:
1. If there are vertical angles they are congruent.
2. If there are corresponding angles between parallel lines, they are congruent.
3. If there are congruent triangles, all their angles are congruent.
The tool we choose will depend on the question - are there parallel lines involved, are there similar triangles, etc.
Remember that since the sum of all angles in a triangle is 180°, to show that all three pairs of angles are the same, it is enough to show that two pairs of angles have the same measure, and the third pair will also be the same, and each one of the angles in the third pair will measure 180° minus the sum of the other two. For short, this is often designated as "Angle-Angle", or AA.
Problem
Line segment DE is parallel to the base, BC, of triangle ΔABC. show that ΔABC∼ ΔADE.
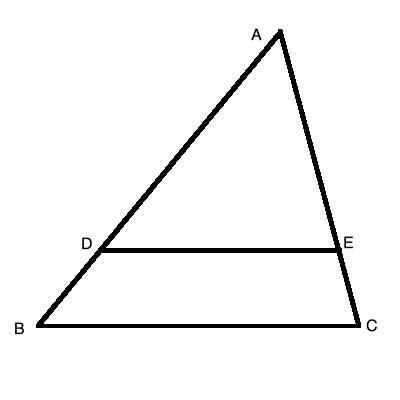
Strategy
Since we are given two parallel lines, this is the hint to use the fact that corresponding angles between parallel lines are congruent.
DE is parallel to BC, and the two legs of the triangle ΔABC form transversal lines intersecting the parallel lines, so the corresponding angles are congruent.
Proof
(1) ∠BAC≅∠DAE //Common angle to both triangles
(2) DE || BC //Given
(3) ∠ABC≅∠ADE //Corresponding angles of two parallel lines intersected by a transversal
(4) ∠ACB≅∠AED //Corresponding angles of two parallel lines intersected by a transversal
(5) ΔABC∼ ΔADE //All three angles are congruent (AAA)
