In today's geometry lesson, we will show that the sum of the interior angles in a pentagon is 540°. And then we will generalize the proof to get a formula that can be used to find the sum of all interior angles for any simple convex polygon.
Problem
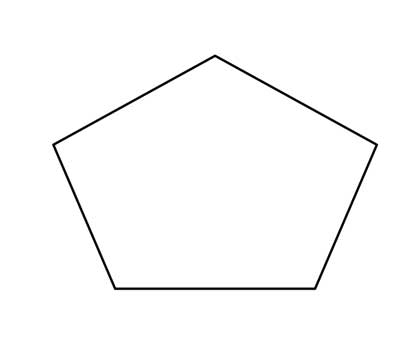
Show that the sum of all interior angles in a simple convex pentagon is 540°.
Strategy
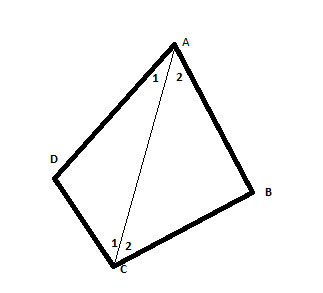
We know that the sum of angles in a triangle is 180°. And we have used this to show that the sum of the interior angles in a simple convex quadrilateral is 360°, by partitioning it into two triangles, where the angles of the triangles make up the angles of the quadrilateral:
We could repeat this strategy here, partitioning the pentagon into a triangle and a quadrilateral, like so:
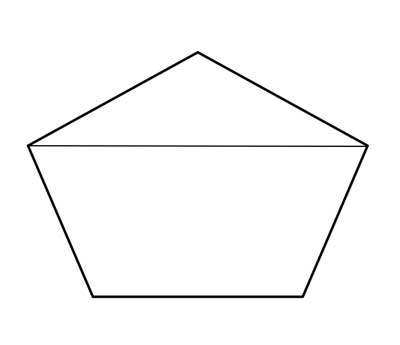
And now, using the fact the triangle's interior angle sum up to 180°, the sum of the interior angles in a simple convex quadrilateral is 360°, and the angle addition postulate, we can add up all the angles of the triangle and the quadrilateral, and see that the sum of all the interior angles in the simple convex pentagon is 180°+ 360°= 540°.
A general strategy for solving this problem
But I want to do a slightly different version of this, which is easier to generalize to a polygon of any number of sides. I will still use the concept of dividing up the polygon into triangles. But this time, I will pick a random point inside the pentagon, and connect it to all the vertices:
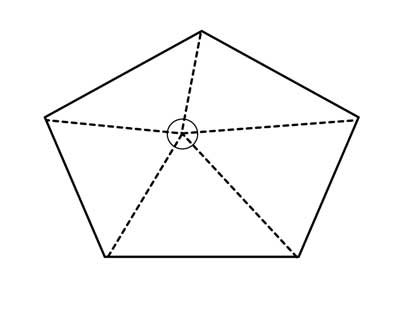
Since we have 5 sides, we will have formed 5 triangles, with each side of the pentagon forming the base of a triangle, and the random interior point we selected forming the apex of each triangle.
Each one of these triangles has a sum of angles of 180°, so 5 of them are 5*180°= 900°. But the 5 apex angles formed around the point we selected are inside the pentagon, and are not part of the sum of its interior angles - so we need to subtract them.
How? Since these 5 angles form a perfect circle around the point we selected, we know they sum up to 360°. So, the sum of the interior angles in the simple convex pentagon is 5*180°-360°=900°-360° = 540°.
It is easy to see that we can do this for any simple convex polygon. Pick a point in its interior, connect it to all its sides, get n triangles, and then subtract 360° from the total, giving us the general formula for the sum of interior angles in a simple convex polygon having n sides as:
n*180-360.
Or , since 360 = 2*180,
(n-2)*180.
