Area of a Rhombus with a 60° angle

If we know the length of a side of a rhombus with a 60° angle, we can find its area in a number of different ways. We will use different properties of parallelograms, diamonds or equilateral triangles. We'll describe several of these methods here.

Problem

A rhombus with side length 10 units has a 60° angle. Find its area.

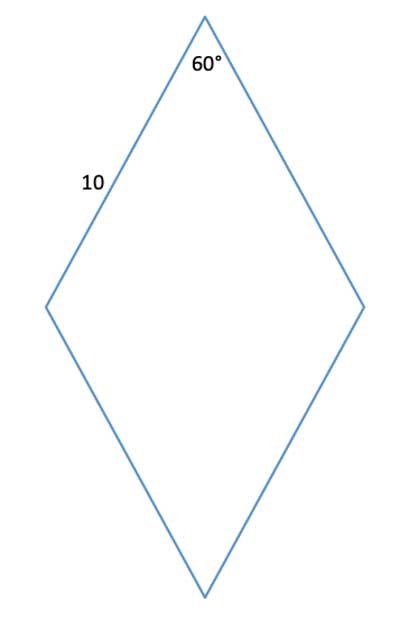
Strategy

Let's start with the most straightforward method for solving this problem. A rhombus is a special type of a parallelogram. We know that the area of any parallelogram is given by the formula A=l·h, where l is the length of one side of the parallelogram and h the height to that side from the opposite side. So let's draw that height:

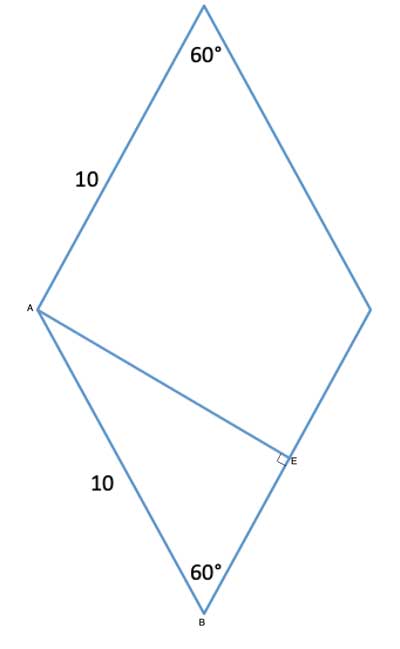
In a parallelogram, the opposite angles are congruent, so m∠ABE =60°. This makes  ΔABE a 30-60-90 triangle.  We know the hypotenuse of this 30-60-90 triangle - it is 10- since all the sides of the rhombus are equal. The long leg of a 30-60-90 triangle, AE, equals half the hypotenuse times √3, so it is 5√3.

AE is the height of the rhombus, and the area of the rhombus is l·h, or 10·5√3= 50√3

Now let's try it a different way:

In a rhombus, the diagonals bisect the angles, and are perpendicular to each other:

This creates 4 right triangles. All are congruent using the Side-Angle-Side postulate: They all have the same length of hypotenuse, all have a common side, and all have a 30° angle.

Each one of these triangles is a 30-60-90 triangle, with a hypotenuse of 10. Their height is 5√3 and their base is 5. So the area of each triangle is (5·5√3)/2. The area of the rhombus is made up of 4 such triangles, so its area is 4·(5·5√3)/2, or 50√3.

One more way to solve this:

Finally, we can think of this rhombus as being composed of 2 equilateral triangles:

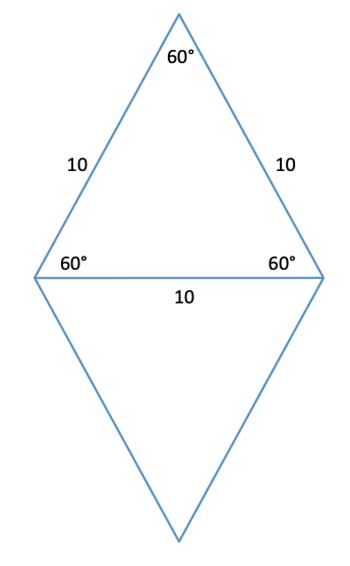
One of the angles is 60°, both sides are equal, so the triangle is isosceles, and so each one of the base angles is (180°-60°)/2=60°.

We have already derived a general formula for the area of an equilateral triangle using the length of its side: Area_{Δequilateral}=(s²*√3)/4

So each of these triangles has an area of (10²*√3)/4 or 25√3, and we have two such triangles, making the area of the rhombus 50√3.