Finding the Area of an Equilateral Triangle from its Perimeter

The perimeter of an equilateral triangle is the length of the three sides of the triangle. Since they are all equal in an equilateral triangle, it is easy to find the area of an equilateral triangle by knowing the perimeter.

Problem

An equilateral triangle has a perimeter of 30 inches. Find its area.

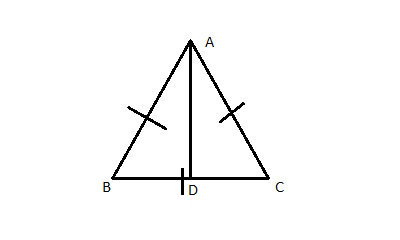
Strategy

So how do you finding the area of an equilateral triangle?

Let's work backwards from the required answer. We need to find the area of a triangle, which is given by the formula Area_Triangle=(Height*Base)/2. So we need to find the length of the base, and the height.

Since all the sides of an equilateral triangle are equal, the base can be any side, and we can easily find the base from the perimeter because the perimeter is simply 3 times the length of any side.

Once we have the length of the side, the height AD can be calculated using the Pythagorean theorem. ΔABD is a right triangle (from the definition of height) and the leg BD is half the length of the side, because ΔABC is an isosceles triangle and in an isosceles triangle, the height to the base bisects the base.

Solution

(1) Perimeter_ΔABC=30   //Given

(2) Perimeter_ΔABC=AB+BC+CA                       //definition of perimeter

(3) AB=BC=CA                                                 //definition of equilateral triangle

(4) Perimeter_ΔABC=BC+BC+BC= 3*BC           //substitution of (3) into (2)

(5) BC = Perimeter_ΔABC/3= 10                        //Algebra

(6) BD = BC/2 = 5                                           //height to base of isosceles triangle bisects the base

(7) ΔABD is a right triangle                             //AD is the height, definition of height

(8) AB²=BD²+AD²                                          //Pythagorean theorem

(9) 10²=5²+AD²                                              //Substitute (6), (5) and (3) into (8)

(10) 100= 25+AD²

(11) 75=AD²

(12) AD= √75

(13) Area_ΔABC=AD*BC/2= √75*10/2=5*√(25*3)=5*5*√3=25*√3

More generally, we can follow the same procedure for an equilateral triangle of any side length, s:

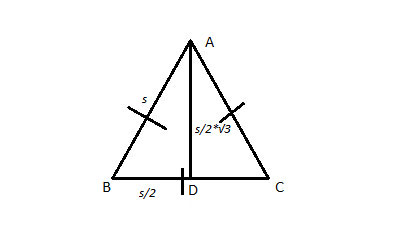
And arrive at the general formula for the area of an equilateral with side s:

Area_{Δequilateral}=(s²*√3)/4

And, if we are given the perimeter, P, rather than the side, s, we get:

Area_{Δequilateral}=[(P/3)²*√3]/4

And we can now just plug in the value for P (or s) to get the area, whenever we see a problem of this type.